| Rozwiązanie równania ruchu cząstki naładowanej w polu magnetycznym |
 |
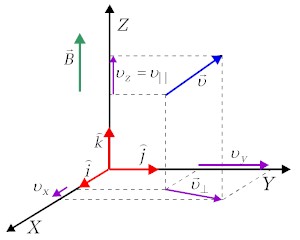
Przypomnijmy, żę układ współrzędnych prostokątnych
ustawmy tak, by
oś Z pokrywała się z kierunkiem wektora indukcji
magnetycznej |
Zapiszemy składowe siły
![]() przedstawiając
iloczyn wektorowy we wzorze
przedstawiając
iloczyn wektorowy we wzorze
|
|
(1) |
w postaci wyznacznika:
|
|
(2) |
Zwróćmy uwagę, że siła w kierunku równoległym do kierunku wektora
indukcji magnetycznej wynosi zero, zaś siły w kierunkach prostopadłych są
wprost proporcjonalne do wartości wektora
![]() ,
przy czym siła w kierunku X jest proporcjonalna do składowej prędkości
w kierunku Y , a siła w kierunku Y do składowej prędkości
w kierunku X.
,
przy czym siła w kierunku X jest proporcjonalna do składowej prędkości
w kierunku Y , a siła w kierunku Y do składowej prędkości
w kierunku X.
Kiedy cząstka spoczywa lub porusza się równolegle do kierunku pola magnetycznego, to nie działa na nią żadna siła pomimo, że znajduje się w polu magnetycznym. Jest to zasadnicza różnica w porównaniu z działaniem na cząstki naładowane pola elektrycznego.
Równania ruchu mają postać
|
. |
(3) |
W równaniach z prawej strony wprowadziliśmy oznaczenie:
|
|
(4) |
Wielkość ![]() odgrywa zasadnicza rolę w zagadnieniu ruchu cząstki naładowanej w polu
magnetycznym i nosi nazwę częstości cyklotronowej.
Zwróćmy uwagę, że wielkość ta pozostaje stała w czasie ruchu jeśli tylko
pozostają stałe: q, B i m. Dla cząstek o tym samym ładunku
lecz różnej masie, poruszających się w tym samym polu magnetycznym, częstość
cyklotronowa jest różna i zależy odwrotnie proporcjonalnie od ich masy.
odgrywa zasadnicza rolę w zagadnieniu ruchu cząstki naładowanej w polu
magnetycznym i nosi nazwę częstości cyklotronowej.
Zwróćmy uwagę, że wielkość ta pozostaje stała w czasie ruchu jeśli tylko
pozostają stałe: q, B i m. Dla cząstek o tym samym ładunku
lecz różnej masie, poruszających się w tym samym polu magnetycznym, częstość
cyklotronowa jest różna i zależy odwrotnie proporcjonalnie od ich masy.
Zapiszmy warunki początkowe, czyli położenie i prędkość cząstki dla t=0
|
|
(5) |
Równania ruchu możemy teraz zapisać w postaci
|
|
(6) |
Skorzystaliśmy tu z faktu, że kiedy pochodna funkcji równa jest zeru, to funkcja równa jest stałej, a za wartości stałych podstawiliśmy wartości prędkości dla t=0.
Z pierwszego z równań po prawej stronie wzoru (6) możemy wyznaczyć y, a następnie pochodną dy/dt,
|
|
|
(7) |
Wstawiając wyrażenie na pochodną dy/dt do drugiego z równań po prawej stronie wzoru (6) otrzymujemy
|
|
co możemy też zapisać w postaci |
|
(8) |
Pamiętając, że wyrażenie
![]() zachowuje wartość stałą w czasie możemy równanie po prawej stronie wzoru (8) przepisać w postaci
zachowuje wartość stałą w czasie możemy równanie po prawej stronie wzoru (8) przepisać w postaci
|
|
(9) |
Równanie powyższe stanowi końcowy wynik pierwszego etapu naszych rozważań. Równanie to jest analogiczne do równania oscylatora harmonicznego, które znamy z kursu Fizyka I, i którego postać i rozwiązanie przytaczamy poniżej
|
równanie oscylatora harmonicznego: |
rozwiązanie równania oscylatora harmonicznego: |
|
|
|
|
(10) |
gdzie ![]() oraz
oraz ![]() są stałymi, które można wyznaczyć z warunków początkowych.
są stałymi, które można wyznaczyć z warunków początkowych.
Rozwiązanie równania (6) ma więc postać
|
|
(11) |
Pochodna względem czasu, czyli prędkość wzdłuż osi X wynosi
|
|
(12) |
Wstawiając to wyrażenie do pierwszego z równań po prawej stronie wzoru (6) otrzymujemy postać rozwiązania równania ruchu dla składowej y. Rozwiązanie dla składowej z, to po prostu równanie ruchu jednostajnie prostoliniowego, co wynika bezpośrednio z postaci trzeciego z równań (6). Ostatecznie, rozwiązanie równań ruchu cząstki w polu magnetycznym w układzie współrzędnych prostokątnych ma postać.
|
|
(13) |
Stałe dowolne
![]() oraz
oraz ![]() wyznaczamy, jak zwykle, z warunków początkowych. Dla współrzędnej x
mamy na podstawie wzorów (13) i (5) dla t=0:
wyznaczamy, jak zwykle, z warunków początkowych. Dla współrzędnej x
mamy na podstawie wzorów (13) i (5) dla t=0:
|
|
(14) |
Dzieląc stronami równanie (b) przez równanie (a) we wzorze (14) otrzymujemy
|
|
(15) |
Widzimy, że faza naszego ruchu harmonicznego, określona jest przez kierunek początkowy rzutu wektora prędkości początkowej na płaszczyznę prostopadłą do kierunku wektora indukcji pola magnetycznego.
Dla wyznaczenia stałej A przekształcimy równanie (a) we wzorze (14)
|
|
(16) |
gdzie skorzystaliśmy z trygonometrycznej równości
![]() .
.
Ostatecznie otrzymujemy równana ruchu cząstki naładowanej w polu magnetycznym, dla warunków początkowych określonych wzorem (5). Są to równania ruchu harmonicznego we współrzędnych X i Y (co odpowiada równaniu okręgu w płaszczyźnie XY) oraz równanie prostej we współrzędnej Z.
|
|
(17) |
Dla znalezienia równania toru podnosimy do kwadratu i dodajemy stronami równania ruchu dla współrzędnych x i y.
|
|
(18) |
Otrzymaliśmy znane z matematyki równanie okręgu.
Tor cząstki w płaszczyźnie prostopadłej do pola jest okręgiem
którego środek znajduje się w punkcie określonym przez współrzędne
![]() oraz
oraz
![]() i o promieniu równym
i o promieniu równym ![]() .
Wartości te określone są wzorami:
.
Wartości te określone są wzorami:
|
|
(19) |
gdzie iloczyn ![]() jest tzw. "składową poprzeczną" pędu cząstki.
jest tzw. "składową poprzeczną" pędu cząstki.