2. Układy współrzędnych i wektor położenia

Przy opisie ruchu posługujemy się pojęciem układu współrzędnych, który wiążemy z wybranym przez nas układem odniesienia. Opis ruchu polega na przyporządkowaniu danemu punktowi   zespołu liczb określających w każdej chwili czasu w jednoznaczny sposób jego położenie w przestrzeni oraz kierunek i wartość jego prędkości i przyspieszenia. Wybór układu odniesienia oraz odpowiedniego układu współrzędnych zależy od rodzaju opisywanego ruchu. Specyfika ruchu często sugeruje wybór odpowiedniego układu współrzędnych.

 
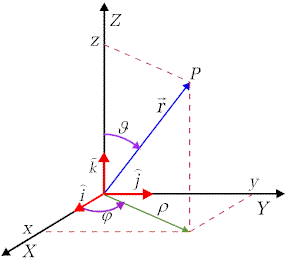Rys. 2.1. Punkt i jego współrzędne w przestrzeni trójwymiarowej.
Na Rys.2.1. pokazane są wielkości określające położenie punktu w przestrzeni trójwymiarowej  za pomocą  wektora położenia (zwanego też promieniem wodzącym). Początek tego wektora znajduje się w początku układu współrzędnych, a koniec w danym punkcie przestrzeni. Na rysunku, dla przykładu, kolorem niebieskim pokazany jest wektor położenia punktu P.  Kolorem czerwonym zaznaczone są wersory, czyli wektory o jednostkowych długościach, określające kierunki osi układu współrzędnych prostokątnych. Symbole omówione będą poniżej.


 Położenie ciała w układzie współrzędnych prostokątnych określone jest przez podanie trzech liczb określających współrzędne wektora położenia względem początku układu na trzech przecinających się w tym punkcie prostopadłych do siebie prostych zwanych osiami . Układ jest prawoskrętny, kiedy obrót osi w kierunku osi wyznacza kierunek osi zgodnie z regułą śruby prawoskrętnej. Pokazany na rysunku układ jest układem prawoskrętnym.

Wektor położenia w układzie prostokątnym jest więc sumą wektorową wersorów pomnożonych przez odpowiadające im składowe promienia wodzącego:

(2.1)

Długość wektora położenia jest liczbą dodatnią i wynosi

(2.2)
Położenie ciała określone jest tu przez podanie długości promienia wodzącego oraz dwóch kątów   i , jakie promień  tworzy z osią i odpowiednio rzut promienia na płaszczyznę   z osią .Wersor współrzędnejskierowany jest zawsze wzdłuż promienia wodzącego, a wersory obu kątów skierowane są w strony określone przez aktualne kierunki ich przyrostów (patrz - Rys.2.2). Jest to istotna różnica pomiędzy układem sferycznym a prostokątnym, gdzie kierunki wersorów są na stałe związane z osiami układu współrzędnych.  
Wektor położenia w układzie sferycznym:

(2.3)
Współrzędne w układzie prostokątnym wyrażone przez współrzędne sferyczne:

(2.4)

Współrzędne w układzie sferycznym wyrażone przez współrzędne prostokątne:

(2.5)

Rys. 2.2. Punkt i jego położenie w układzie współrzędnych sferycznych.

Układ współrzędnych sferycznych będziemy stosować do opisu ruchu ciał wokół zadanego punktu w przestrzeni trójwymiarowej i w przypadkach, kiedy siły działające w przestrzeni mają symetrię sferyczną.

W układzie tym położenie ciała określone jest przez podanie długości rzutu promienia wodzącego na płaszczyznę  oznaczonego jako , kąta   jaki tworzy rzut z osią oraz współrzędnej  .  Wersor współrzędnej   skierowany jest zawsze wzdłuż kierunku rzutu promienia wodzącego na płaszczyznę , kierunek wersora kąta  określony jest przez aktualny kierunek  zmiany tego kąta, wersor współrzędnej zachowuje stały kierunek, podobnie jak w układzie współrzędnych prostokątnych. (patrz Rys.2.3)
Wektor położenia w układzie współrzędnych cylindrycznych:

(2.6)
Współrzędne w układzie prostokątnym wyrażone przez współrzędne cylindryczne:

(2.7)

Współrzędne w układzie cylindrycznym wyrażone przez współrzędne prostokątne:

(2.8)

Rys. 2.3. Punkt i jego położenie w układzie współrzędnych cylindrycznych.

Układ współrzędnych cylindrycznych będziemy stosować do opisu ruchu ciał wokół zadanej osi w przestrzeni trójwymiarowej i w przypadkach, kiedy siły działające w przestrzeni mają symetrię walcową.

Kiedy ruch odbywa się w jednej płaszczyźnie nazywamy go ruchem płaskim. Możemy zawsze tak dobrać osie układu współrzędnych, by odbywał się w płaszczyźnie przez nas zadanej, np. .  Ruch płaski możemy traktować jako szczególny przypadek ruchu przestrzennego, kiedy w układzie prostokątnym i cylindrycznym współrzędna  równa jest zeru, a w układzie sferycznym kąt J  równy jest p/2.

Do opisu ruch płaskiego stosujemy często układ współrzędnych biegunowych. W układzie tym położenie punktu wyrażone jest przez dwie liczby: długość promienia wodzącego r i kąt obrotu j, liczony względem osi X. Wersor promienia wodzącego skierowany jest wzdłuż jego kierunku; wersor kąta j jest  do niego prostopadły (patrz Rys.2.4)

 
Wektor położenia w układzie współrzędnych biegunowych:

(2.9)
Współrzędne w dwuwymiarowym układzie prostokątnym wyrażone przez współrzędne biegunowe:


(2.10)
Współrzędne w układzie biegunowym wyrażone przez współrzędne prostokątne:


(2.11)

Rys. 2.4. Punkt i jego położenie w układzie współrzędnych biegunowych.

Układ współrzędnych biegunowych będziemy stosować do opisu ruchu ciał wokół zadanego punktu  w przestrzeni dwuwymiarowej i w przypadkach, kiedy siły działające w płaszczyźnie mają symetrię obrotową.