.
Siła oddziaływania grawitacyjnego należy do grupy sił zwanych siłami centralnymi. Siła centralna to taka, która skierowana jest stale do lub od tego samego punktu zwanego środkiem lub centrum siły. Ogólnie, siły centralne, które zależne są tylko od odległości od centrum siły, można wyrazić w postaci
|
|
(8.20) |
Znak (+) oznacza siły skierowane od centrum pola, znak (-) do centrum pola.
Z definicji tej widać natychmiast, że w przypadku siły centralnej moment siły względem jej centrum równy jest zeru. Z zasady zachowania momentu pędu wynika natomiast, że wtedy moment pędu punktu materialnego względem centrum zachowuje stałą wartość.
 |
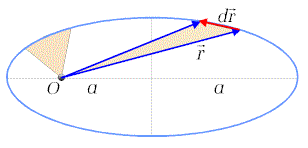Wykorzystamy te własności rozpatrując ruch punktu
materialnego o masie m pod działaniem siły centralnej.
Rysunek 8.5 Fragment toru z zaznaczonym centrum O, promieniem wodzącym r oraz elementarnym przemieszczeniem dr |
Pamiętając, że 
możemy napisać
|
|
(8.21) |
Długość określonego w ten sposób wektora 
równa jest polu trójkąta, który zakreśla promień wodzący poruszającego
się punktu w czasie dt. Pochodna wektora 
względem
czasu
|
|
(8.22) |
nosi nazwę prędkości polowej. Wykorzystując wzór (8.21) widzimy, że
|
|
(8.23) |
Pamiętamy jednak, że w rozpatrywanym przez nas ruchu pod działaniem siły
centralnej moment pędu 
zachowuje wartość stałą. Oznacza to, że i prędkość polowa pozostaje w
tym ruchu stała. W konsekwencji, stałe pozostają też pola zakreślane w
jednakowych odcinkach czasu przez promień wodzący poruszającego się takim
ruchem punktu.
Ze stałości momentu pędu ciała poruszającego się pod działaniem siły centralnej wynika jeszcze jeden interesujący fakt. Ruchy ciał w takim polu zachodzą zawsze w jednej płaszczyźnie wyznaczonej przez wektor wodzący ciała (wyprowadzony z centrum pola) i wektor pędu z jakim ciało wkracza do pola.
Można wykazać, że pod wpływem siły centralnej ciała poruszają się po tzw. krzywych stożkowych: elipsie, paraboli lub hiperboli. Planety, poruszające się w polu grawitacyjnym Słońca, zakreślają tory eliptyczne, które z wyjątkiem Plutona są bardzo zbliżone do okręgów. Niektóre komety poruszają się po orbitach hiperbolicznych lub parabolicznych. Centrum siły znajduje się w punkcie zwanym ogniskiem krzywej. Oczywiście, planety także zakreślają w jednakowych odcinkach czasu jednakowe pola.
Z prawa grawitacji wynika jeszcze jedna prawidłowość ruchu planet. Siła grawitacji pełni funkcję siły dośrodkowej i właśnie dzięki temu planety krążą wokół Słońca. Przyjmując, że ruch odbywa się po orbicie kołowej możemy przyrównać siłę grawitacji do siły dośrodkowej otrzymując
|
|
(8.24) |
gdzie 
i 
są
odpowiednio masami planety i Słońca; 
jest odległością planety od Słońca, a 
okresem jej obiegu wokół Słońca. Ze związku (8.24) wynika że
|
|
(8.25) |
Stała ta nie jest zależna od masy planety więc relacja pomiędzy odległością planety od słońca i okresem jej obiegu może być zastosowana do dowolnej planety. Stosując ją dla dwóch planet otrzymujemy związek.
|
|
(8.26) |
Przedstawione tu prawidłowości zostały sformułowane przez Keplera w latach 1609-1619 w postaci trzech praw zwanych prawami Keplera.
Prawa te można wyrazić następująco:
.
.