Dotychczas rozważaliśmy ruch harmoniczny swobodny, w którym nie występowały żadne siły tłumiące. Na ogól jednak ruch jest tłumiony wskutek oporu powietrza lub innych oporów występujących w układzie drgającym. Opory te zwykle są proporcjonalne do prędkości ciała. Siła działająca na ciało zawiera więc dodatkowy człon proporcjonalny do prędkości. Parametr b, jest współczynnikiem proporcjonalności.
| (6.24) |
Równanie ruchu ma teraz postać:
| (6.25) |
Rozwiązaniem tego równania jest wyrażenie:
| (6.26) |
gdzie b =b/2m zwane jest współczynnikiem tłumienia. Szczegóły rozwiązania równania ruchu oscylatora harmonicznego tłumionego można znaleźć w referencji 3 bibliografii.
Częstość drgań tłumionych w1
wynosi: Wpółczynnik tłumienia
Zwróćmy uwagę, że współczynnik tłumienia b
=b/2m
rośnie proporcjonalnie do wzrostu oporów ruchu ale
jest też odwrotnie proporcjonalny do masy drgającego ciała. Im większa jest
masa ciała tym mniejszy wpływ na ruch drgający mają opory ruchu. Współczynnik
tłumienia modyfikuje zarówno częstość jak i amplitudę drgań zgodnie z
wzorami podanymi poniżej.
| (6.27) |
Częstość ta jest mniejsza niż częstości drgań własnych układu swobodnego. W konsekwencji zwiększa się okres drgań, T1.
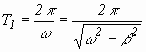
| (6.28) |
|---|
Amplituda drgań, A1 zmniejsza się z czasem w sposób wykładniczy:
| (6.29) |
Amplitudy dla kolejnych okresów drgań będą:
| (6.30) |
Biorąc stosunek dwóch kolejnych amplitud otrzymujemy:
| (6.31) |
Logarytm tego stosunku nazywamy logarytmicznym dekrementem tłumienia, d.
| (6.32) |
Zależność amplitudy od czasu w kolejnych okresach drgań możemy więc zapisać jako:
| (6.33) |
Warto zwrócić uwagę, że kiedy tłumienie będzie rosło, w konsekwencji czego wyrażenie (6.33) osiągnie wartość zero, a okres drgań będzie nieskończony - ruch nasz przestanie być ruchem okresowym. Takie tłumienie nazywamy krytycznym. Ten przypadek graniczny odpowiada sytuacji, w której układ nasz najszybciej osiąga położenie równowagi. Przy dalszym wzroście współczynnika tłumienia ruch będzie miał charakter aperiodyczny (pełzający). Układ będzie zdążał do położenia równowagi, ale wolniej niż w przypadku granicznym. Określenie warunków, w których ruch drgający zmienia się w ruch aperiodyczny odgrywa istotną rolę w konstrukcji układów, gdzie ważne jest tłumienie niepożądanych drgań: przyrządy pomiarowe, amortyzatory itp.
Kliknij w polu rysunku.
MS-Excel
Interaktywna
ilustracja graficzna
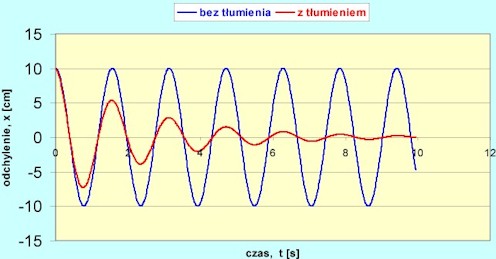
Rys.6.4.Drgania harmoniczne proste i tłumione.