Rch ciał o zmiennej masie

Fot.3.3. Start rakiety na poligonie doświadczalnym
(WiŻ, 5, 2001r)
|
Można podać wiele przykładów ruchu ciał o zmiennej
masie. Najczęściej wymienianym jest ruch wznoszącej się rakiety. Ruch
o zmiennej masie występuje też w pracy taśmociągów transportujących
sypki materiał. Takim ruchem jest ruch kropelek wody rzuconych na gorącą
powierzchnię lub bryły lodu pływającej w wodzie. Wreszcie - kończąc
żartobliwie - ruch kuli śniegowej, kiedy lepimy bałwana. W jednych
przypadkach masa ciała zwiększa się, w innych ulega zmniejszeniu, w
jeszcze innych, oba procesy mają miejsce równocześnie.
|
|
|
|

|
|
| Dla ustalenia uwagi rozpatrzmy
ruch startującej pionowo rakiety.
Przyjmijmy, że rakieta startuje w chwili t=0 i wtedy jej prędkość
wynosi zero a masa równa jest m0. Masę rakiety po czasie
t od chwili startu oznaczmy przez mr, a jej
prędkość w nieruchomym układzie odniesienia przez u
r. Masę gazów wyrzucanych w czasie dt oznaczmy przez dmg,
a ich prędkość względem rakiety przez ugr.
Zapiszmy pęd naszego układu w chwilach czasu t oraz t+dt.
Stosujemy zapis skalarny bowiem pionowy ruch jest ruchem jednowymiarowym.
|
Pęd zapisujemy w nieruchomym układzie współrzędnych.
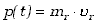
| 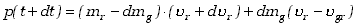
| (3.27)
|
gdzie du r jest przyrostem prędkości
rakiety. Zmiana pędu rakiety w odcinku czasu dt
będzie
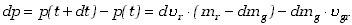
| (3.28)
|
(Sprawdź to, podstawiając odpowiednie wyrażenia z wzorów
(3.10) i dokonując elementarnych przekształceń.)
Zwróćmy tu uwagę, że przyrost pędu będzie równy zeru jeśli w naszym
układzie nie występują siły zewnętrzne, co jest prostą konsekwencją zasad
dynamiki. Zauważmy też, że w wyrażeniu (mr - dmg)
masa gazów wyrzucanych w czasie dt jest znacznie mniejsza niż masa
całej rakiety i może być spokojnie pominięta. (Oczywiście, nie
możemy jej pominąć w wyrażeniu dmg×
ugr , bowiem od niczego nie jest tam
odejmowana.)
Zmianę pędu możemy więc zapisać w prostszej formie
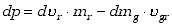
| (3.29)
|
Skoro znamy wyrażenie na przyrost pędu możemy, dzieląc obie strony wyrażenia
(3) przez przyrost czasu dt, zapisać drugą zasadę dynamiki dla naszego
przypadku:
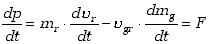 , ,
| (3.30)
|
Równanie ruchu ma więc postać
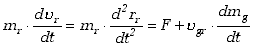
| (3.31)
|
W ten sposób sformułowaliśmy równanie ruchu dla ogólnego przypadku, kiedy
masa ciała w czasie ruchu ulega zmianie, ubywająca masa odrzucana jest z prędkością
ugr, a na ciało działa zewnętrzna
siła F. Zauważmy, że ilość wyrzucanych gazów dmg/dt,
pomnożona przez ich prędkość względem rakiety stanowi dodatkową siłę w
naszym równaniu ruchu. To właśnie ta siła sprawia, że rakieta zwiększa swą
prędkość, dlatego często nazywa się ja siła ciągu. Siła F
reprezentuje siły zewnętrzne działające na ciało. W naszym przypadku są to
siły grawitacji i oporów ruchu działające w kierunku przeciwnym niż siła
ciągu.
Zwróćmy także uwagę, że wyrażenie dmg/dt
to po prostu masa gazów wyrzucanych w jednostce czasu, którą możemy wyrazić
na przykład w kg/s. Przyjmijmy, że przez cały czas lotu
rakieta spala stałą ilość paliwa w jednostce czasu. Niech będzie to dmg/dt=ng
kilogramów na sekundę. Masa rakiety w funkcji czasu t wyniesie wtedy
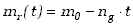
| lub
| 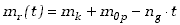
| (3.32)
|
gdzie wydzieliliśmy masę korpusu rakiety symbolem mk i początkową
masę paliwa symbolem m0p. Zauważmy również, że kiedy
masa rakiety zmniejsza się w czasie ruchu, to jej ubytek dmr równy
jest masie wyrzucanych gazów, ale wzięty z przeciwnym znakiem czyli
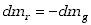
| (3.33)
|
Przyjmijmy teraz dla uproszczenia naszych rozważań, że siła ciągu jest o
wiele większa od sił oporów ruchu i sił grawitacji . Wówczas w
równaniu ruchu można pominąć siłę F otrzymując prostsze równanie
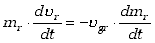
|
lub równoważne mu
| 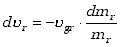
| (3.34)
|
Jest to równanie różniczkowe o rozdzielonych zmiennych, co umożliwia całkowanie
niezależne lewej i prawej strony w granicach odpowiadających temu samemu
przedziałowi czasu
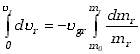
| (3.35
|
W rezultacie otrzymujemy
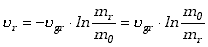
| (3.36)
|
W ten sposób uzyskujemy wzór na prędkość rakiety po czasie t.
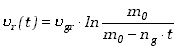
| (3.37)
|
Uzyskaliśmy słynny wzór Ciołkowskiego wyprowadzony na długo przed rozwojem
techniki rakietowej.
Pamiętając, że przyspieszenie jest pochodną prędkości względem czasu
otrzymujemy wyrażenie na przyspieszenie rakiety w funkcji czasu
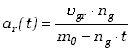 . .
| (3.38)
|
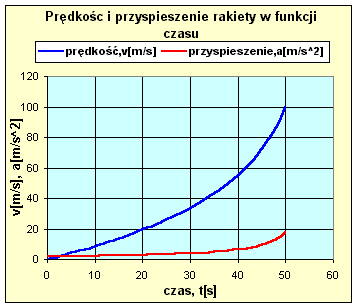 |
Zwróćmy uwagę, że w początkowej fazie lotu rakiety
przyspieszenie wzrasta nieznacznie, bowiem wyrażenie w liczniku wzoru
(3.38) ma wartość stałą, a masa rakiety na starcie jest znacznie
większa od masy wyrzucanych gazów. W rezultacie, wzrost prędkości
jest prawie liniowy. W końcowej fazie, kiedy wyrażenie w mianowniku
wzoru (3.38) zbliża się do masy korpusu rakiety, przyspieszenie wzrasta,
wskutek czego wzrost prędkości jest szybszy od liniowego. Dla
zmniejszenia masy korpusu buduje się rakiety wieloczłonowe. Wykorzystane
pojemniki na paliwo zostają odrzucane w czasie lotu. |
| Rys. 3.1.Przykładowe zmiany prędkości
i przyspieszenia rakiety w czasie lotu. |
|
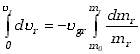
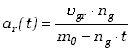 .
.
