Przemiany jądrowe |
Przez przemianę jądrową rozumiemy przekształcenie się danego jądra
atomowego w inne jądro w połączeniu z emisją cząstki
![]() (jądra
helu
(jądra
helu ![]() ),
),
![]() (elektronu
albo pozytonu)
lub
(elektronu
albo pozytonu)
lub ![]() (fotonu).
Nazwa przemiany określona jest przez nazwę emitowanej cząstki. Za przemianę
(fotonu).
Nazwa przemiany określona jest przez nazwę emitowanej cząstki. Za przemianę
![]() uważa się także wychwyt elektronu
uważa się także wychwyt elektronu
![]() z powłoki atomowej.
z powłoki atomowej.
Kiedy wyemitowana jest cząstka
![]() ,
to przekształcane jądro ma liczbę masową mniejszą o 4 i liczbę atomową
mniejszą o 2.
,
to przekształcane jądro ma liczbę masową mniejszą o 4 i liczbę atomową
mniejszą o 2.
| (5.3.1) |
W przemianie
![]() liczba masowa się nie zmienia, a liczba atomowa zmienia się o jeden:
liczba masowa się nie zmienia, a liczba atomowa zmienia się o jeden:
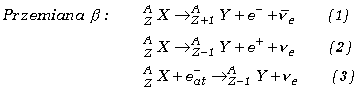 |
(5.3.2) |
W przemianie ![]() obie
liczby pozostają niezmienione, zmienia się natomiast energia wzbudzenia jądra
obie
liczby pozostają niezmienione, zmienia się natomiast energia wzbudzenia jądra
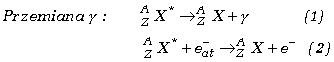 |
(5.3.3) |
Przemiany zachodzące samorzutnie nazywamy naturalnymi przemianami jądrowymi, a izotopy pierwiastków ulegających przemianom naturalnym nazywamy promieniotwórczymi. Pierwsze przemiany promieniotwórcze zostały zaobserwowane przez Becquerella w 1896 roku, a następnie przez Marię Skłodowską-Curie i Pierre'a Curie w 1898 roku. Można uzyskać także izotopy promieniotwórcze drogą reakcji jądrowych. Pierwsze izotopy promieniotwórcze zostały otrzymane przez Irenę i Fryderyka Joliot-Curie. Obecnie znamy ponad 2000 izotopów, spośród których tylko 267, to izotopy trwałe, zaś pozostałe - to izotopy promieniotwórcze.
Przemiana promieniotwórcza, zwana także rozpadem promieniotwórczym, jest procesem statystycznym. Oznacza to, że nie można przewidzieć w której chwili dane jądro ulegnie rozpadowi, można natomiast określić prawdopodobieństwo tego rozpadu. Rozpady poszczególnych jąder następują niezależnie od siebie. Liczba jąder, które ulegną rozpadowi w krótkim przedziale czasu proporcjonalna jest do liczby jąder N i do długości przedziału czasu, dt
| (5.3.4) |
gdzie![]() jest współczynnikiem proporcjonalności zwanym stałą rozpadu.
Znak minus we wzorze (5.3.4) oznacza, że liczba jąder ulegających rozpadowi
jest współczynnikiem proporcjonalności zwanym stałą rozpadu.
Znak minus we wzorze (5.3.4) oznacza, że liczba jąder ulegających rozpadowi
![]() ,
odejmuje się od liczby jąder N. Dzieląc obie strony tego
wzoru przez N uzyskujemy równanie różniczkowe, które można
łatwo scałkować
,
odejmuje się od liczby jąder N. Dzieląc obie strony tego
wzoru przez N uzyskujemy równanie różniczkowe, które można
łatwo scałkować
| (5.3.5 |
gdzie C jest stałą całkowania. Oznaczając przez N0 liczbę
jąder w chwili początkowej tj. dla t=0 możemy wyznaczyć
stałą całkowania:![]() .
Liczba jąder, które nie rozpadły się w czasie t wynosi
więc
.
Liczba jąder, które nie rozpadły się w czasie t wynosi
więc
| (5.3.6) |
Wzór (5.3.6) wyraża prawo rozpadu promieniotwórczego - podstawowe prawo przemian jądrowych. Liczba jąder, które uległy rozpadowi w czasie t wynosi
| (5.3.7) |
Średni czas życia jądra promieniotwórczego
![]() równy jest odwrotności stałej rozpadu;
równy jest odwrotności stałej rozpadu;
![]() .
Czas, w którym rozpadowi ulega połowa początkowej liczby jąder nazywany
jest czasem połowicznego zaniku. Czas ten wyznaczyć można za związku
.
Czas, w którym rozpadowi ulega połowa początkowej liczby jąder nazywany
jest czasem połowicznego zaniku. Czas ten wyznaczyć można za związku
| (5.3.8) |
Liczba rozpadów zachodzących w jednostce czasu w źródle promieniotwórczym nosi nazwę aktywności A. Aktywność źródła określona jest więc jako stosunek liczby rozpadów w danym przedziale czasu do wielkości tego przedziału, patrz wzór (5.3.4),
| (5.3.9) |
Jednostką aktywności jest bekerel (Bq). Jeden bekerel, to aktywność źródła, w którym zachodzi jeden rozpad na sekundę. Zanik aktywności źródła określony jest przez prawo rozpadu promieniotwórczego.
Jądra powstające w wyniku przemian jądrowych są często także promieniotwórcze, choć charakteryzują się innym czasem życia. Prowadzi to do tworzenia się tzw. łańcucha lub szeregu promieniotwórczego złożonego z wielu przemian alfa i beta, a kończącego się na jądrze stabilnym czyli takim, które już dalej się nie rozpada. Naturalne przemiany promieniotwórcze tworzą cztery szeregi, których nazwy pochodzą od nazw pierwszych izotopów danego szeregu. Szeregi te tworzą rodziny izotopów, których liczby masowe wyrazić można wzorem
| (5.3.10) |
bowiem w każdej przemianie
![]() liczba masowa zmienia się o cztery, a w przemianie
liczba masowa zmienia się o cztery, a w przemianie
![]() nie zmienia się.
nie zmienia się.
| Nazwa szeregu | A | Izotop początkowy | Izotop końcowy | T1/2, lat |
| torowy | 4n | 23290Th | 20882Pb | 1.4*1010 |
| neptunowy | 4n+1 | 23793Np | 20983Bi | 2.2*106 |
| uranowo-radowy | 4n+2 | 23892U | 20682Pb | 4.5*109 |
| uranowo-aktynowy | 4n+3 | 23592U | 20782Pb | 7.2*108 |
Czasy życia pośrednich izotopów szeregu są zwykle znacznie krótsze, ale istnienie danego szeregu określone jest przez czas życia pierwszego izotopu w łańcuchu. Dlatego w przyrodzie nie występują już naturalne izotopy szeregu neptunowego, bowiem czas życia izotopu 23793Np (2.2*106 lat) jest znacznie krótszy od wieku Ziemi, który szacuje się na 109 lat.
Fakt, że nie można przewidzieć, które jądro ulegnie w danym czasie rozpadowi sprawia, że rejestrując cząstki pochodzące z
rozpadów jądrowych w jednakowych odcinkach czasu rejestrujemy różną ich liczbę. Wykonując wielokrotnie pomiar liczby rozpadów w
zadanym odcinku czasu otrzymujemy pewien rozkład liczby rozpadów. Rozkład ten bardzo dobrze opisuje funkcja teoretyczna zwana rozkładem
Poissona. Można pokazać, że rozkład Poissona stosuje się do opisu takich procesów statystycznych, które stanowią zdążającą do
nieskończoności sumę n zdarzeń elementarnych*) zachodzących ze zdążającym do zera prawdopodobieństwem
p, podczas gdy iloczyn ![]() pozostaje stały. Rozkład Poissona ma następującą postać:
pozostaje stały. Rozkład Poissona ma następującą postać:
| (5.3.11) |
Wzór ten podaje prawdopodobieństwo zajścia k zdarzeń w rozkładzie Poissona dla którego wartość przeciętna wynosi ![]() .
Dla przykładu, rozkładem Poissona można opisać liczbę klientów wchodzących do danego sklepu w danym odcinku czasu np. 5-ciu minut. Można
uznać, że liczba n osób (np. w Warszawie), które mogą do tego sklepu wejść jest bardzo duża, ale prawdopodobieństwo ,p,
że dana konkretna osoba, (np. ja) wejdzie do tego sklepu w danym pięciominutowym odcinku czasu jest bardzo małe. Znacznie bardziej jednoznaczna
sytuacja jest w przypadku rozpadu promieniotwórczego. Liczba jąder, n, w preparacie promieniotwórczym, które mogą ulec
rozpadowi w danym odcinku czasu jest ogromna, ale prawdopodobieństwo rozpadu pojedynczego jądra, p, jest bardzo małe.
Znakomicie spełnione są wiec warunki stosowalności rozkładu Poissona.
.
Dla przykładu, rozkładem Poissona można opisać liczbę klientów wchodzących do danego sklepu w danym odcinku czasu np. 5-ciu minut. Można
uznać, że liczba n osób (np. w Warszawie), które mogą do tego sklepu wejść jest bardzo duża, ale prawdopodobieństwo ,p,
że dana konkretna osoba, (np. ja) wejdzie do tego sklepu w danym pięciominutowym odcinku czasu jest bardzo małe. Znacznie bardziej jednoznaczna
sytuacja jest w przypadku rozpadu promieniotwórczego. Liczba jąder, n, w preparacie promieniotwórczym, które mogą ulec
rozpadowi w danym odcinku czasu jest ogromna, ale prawdopodobieństwo rozpadu pojedynczego jądra, p, jest bardzo małe.
Znakomicie spełnione są wiec warunki stosowalności rozkładu Poissona.
Wartość przeciętna ![]() ,
która w przypadku wykonywanych pomiarów przybliżana (estymowana) jest przez wartość średnią, jest jedynym parametrem w
rozkładzie Poissona. Ważną własnością tego rozkładu jest to, że odchylenie standardowe, które charakteryzuje "szerokość"
rozkładu, równe jest pierwiastkowi z wartości przeciętnej tzn.
,
która w przypadku wykonywanych pomiarów przybliżana (estymowana) jest przez wartość średnią, jest jedynym parametrem w
rozkładzie Poissona. Ważną własnością tego rozkładu jest to, że odchylenie standardowe, które charakteryzuje "szerokość"
rozkładu, równe jest pierwiastkowi z wartości przeciętnej tzn.
| (5.3.11) |
Względna "szerokość" rozkładu, którą określimy jako stosunek wartości odchylenia standardowego do wartości przeciętnej wynosi więc
| (5.3.11) |
Widzimy, że względna szerokość rozkładu maleje ze wzrostem wartości przeciętnej w rozkładzie Poissona.
Inną ważną własnością rozkładu Poissona jest to, że rozkład ten, który dla małych wartości przeciętnych jest silnie
asymetryczny, staje się coraz bardziej symetryczny wraz ze wzrostem parametru ![]() .
Rozkład ten dla większych wartości przeciętnych może więc być dobrze przybliżany przez znany z analizy niepewności przypadkowych
rozkład Gaussa (normalny). Zauważmy jednak, że rozkład Gaussa zależny jest od dwóch parametrów: wartości przeciętnej
(oczekiwanej)
.
Rozkład ten dla większych wartości przeciętnych może więc być dobrze przybliżany przez znany z analizy niepewności przypadkowych
rozkład Gaussa (normalny). Zauważmy jednak, że rozkład Gaussa zależny jest od dwóch parametrów: wartości przeciętnej
(oczekiwanej) ![]() ,
oraz odchylenia standardowego
,
oraz odchylenia standardowego ![]() (patrz wzór (1.2.1) w wykładzie pierwszym semestru drugiego). Przybliżając więc rozkładem Gaussa rozkład Poissona musimy tak dobrać
wartość parametru
(patrz wzór (1.2.1) w wykładzie pierwszym semestru drugiego). Przybliżając więc rozkładem Gaussa rozkład Poissona musimy tak dobrać
wartość parametru ![]() ,
by spełniony był warunek (5.3.11) tj. by
,
by spełniony był warunek (5.3.11) tj. by ![]() .
Zwróćmy też uwagę, że rozkład Poissona określony jest tylko do dla całkowitych i nieujemnych wartości argumentu k,
podczas gdy rozkład Gaussa określony jest dla wszystkich wartości zmiennej rzeczywistej.
.
Zwróćmy też uwagę, że rozkład Poissona określony jest tylko do dla całkowitych i nieujemnych wartości argumentu k,
podczas gdy rozkład Gaussa określony jest dla wszystkich wartości zmiennej rzeczywistej.
--------------------------------------------------------------------
*) Przez zdarzenie elementarne rozumiemy tu takie zdarzenie losowe, które ma dwie możliwości, albo zajść albo nie zajść; np. w
rzucie monetą wyrzucenie reszki może zajść lub nie. Bardziej złożona jest sytuacja w rzucie kostką do gry; wtedy jest sześć możliwości,
choć można zdarzenie elementarne zdefiniować tak by było ich dwie, np. wyrzucenie lub nie wyrzucenie czterech oczek, albo liczby oczek więcej
niż dwa itp.