Wiemy już jak wyznaczyć położenie punktu materialnego w
przestrzeni trójwymiarowej
posługując się układem współrzędnych prostokątnych.
Ruch - to jednak zmiana tego położenia w czasie, co oznacza, że zarówno
długość jak i kierunek wektora położenia są funkcją czasu t.
Zapiszemy to następująco:
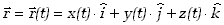
| (2.12)
|
Podobnie zapisać możemy przyrost wektora położenia w zadanym
przedziale czasu
Dt.
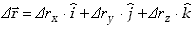
| (2.13)
|
Zmianę położenia na jednostkę czasu otrzymamy przez podzielenie przyrostu
wektora położenia przez przyrost czasu:
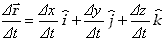
| (2.14)
|
Kiedy przyrost czasu zdąża do zera, nasz iloraz różnicowy (13) przechodzi w
pochodną wektora położenia względem czasu.
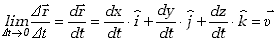
| (2.15)
|
Pochodna wektora położenia względem czasu w zadanej chwili
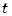 nazywa się
prędkością chwilową ciała
nazywa się
prędkością chwilową ciała
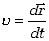 . .
| (2.15a)
|
Z matematyki wiemy, że pochodna wyznaczona jest
przez styczną do funkcji w danym punkcie. Naszą funkcją jest położenie ciała, a
zmiana tego położenia w czasie wyznacza tor ciała w przestrzeni. Oznacza to, że
wektor prędkości chwilowej pokrywa się ze styczną do toru w danym punkcie a jego
zwrot wyznaczony jest przez znak przyrostu wektora położenia.
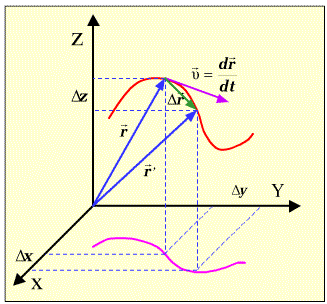
Na rysunku obok kolorem czerwonym pokazany jest przykładowy tor ciała w przestrzeni.
Rzut toru na płaszczyznę poziomą pokazany jest kolorem różowym.
Kolorem niebieskim zaznaczone są promienie wodzące dla dwóch punktów na torze, a
kolorem zielonym ich różnica, czyli przyrost wektora położenia.
|
Na osiach układu współrzędnych zaznaczone są jego składowe. Zmiana położenia
odbywa się w czasie, a więc każdemu punktowi na torze odpowiada określony czas. Kiedy różnica czasu
zmierza do zera wektory położenia zbliżają się do siebie, a iloraz przyrostu
wektora położenia do przyrostu czasu zmierza do skończonej wartości, która
jest właśnie prędkością chwilowa naszego ciała. Wektor prędkości zaznaczony jest kolorem fioletowym.
Wektor ten jest styczny do toru ciała w każdym jego punkcie.
|
| Rys. 2.5.
Przykładowy tor ciała w przestrzeni. |
|
Jednostką prędkości w układzie SI jest prędkość ciała poruszającego się ruchem jednostajnym, które w
ciągu jednostki czasu (sekundy) przebywa jednostkę długości (metr). Jednostkę
prędkości zapisujemy w postaci 1 m/s .
Wspominaliśmy już, że specyfika ruchu sugeruje wybór odpowiedniego układu
współrzędnych. Kiedy analizujemy ruch pasażera pędzącego pociągu widać celowość
zastosowania dwuwymiarowego układu prostokątnego i wybór osi wzdłuż i w
poprzek kierunku ruchu pociągu. Kiedy jednak pociąg zakręca i jedzie po łuku
będącym elementem okręgu, może okazać się przydatne wykonać analizę w układzie
biegunowym. Kiedy jeszcze dodatkowo nasz pociąg pokonuje wzniesienie - wybór
układu sferycznego lub cylindrycznego może być uzasadniony.
Zdefiniowany już wcześniej wektor prędkości w układzie współrzędnych
prostokątnych możemy zapisać jako.
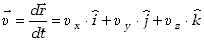
| (2.16)
|
gdzie składowe prędkości wynoszą
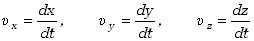
| (2.17)
|
Forma tego zapisu jest analogiczna do zapisu wektora położenia, tylko wartości
współrzędnych zastąpiliśmy wartościami składowych wektora prędkości.
Wartość bezwzględną wektora prędkości wyrażoną przez jej składowe w układzie
kartezjańskim zapiszemy analogicznie do wzoru (2)
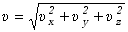
| (2.18)
|
Zwróćmy uwagę, że w życiu codziennym właśnie wartość bezwzględną (moduł)
prędkości nazywamy "prędkością"
lub "szybkością" nie interesując się na ogół kierunkiem tego wektora.
Zapiszmy teraz wektor prędkości w układzie współrzędnych biegunowych.
Definicja tego układu podana jest wyżej.
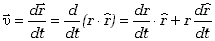
| (2.19)
|
Najpierw zapisaliśmy wektor położenia w układzie biegunowym,
potem zastosowaliśmy regułę liczenia pochodnej iloczynu funkcji .
Otrzymaliśmy dwie składowe wektora prędkości. Pierwsza skierowana jest
wzdłuż kierunku promienia wodzącego wyznaczonego przez jego wersor.
Druga zawiera iloczyn wektora położenia i pochodnej wersora promienia wodzącego
względem czasu.
|
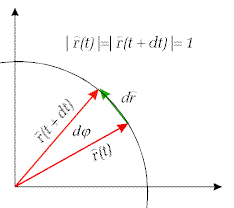
Pamiętamy, że wersor jest wektorem i pomimo stałej
(jednostkowej) wartości bezwzględnej, jego kierunek może się zmieniać.
Kierunek ten pokrywa się z kierunkiem zmiany kąta
j, co ilustruje rysunek obok.
Wykorzystując fakt, że długość wersora wynosi 1 otrzymujemy zależność: |
|
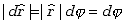
|
(2.20)
|
|
(Skorzystaliśmy tu z definicji kąta wyrażonego w mierze łukowej jako
stosunku długości łuku do wartości promienia odpowiadającego mu okręgu.)
|
|
Rys.2.6. Zmiana kierunku wersora. |
|
Pochodną wersora promienia wodzącego względem czasu możemy wiec zapisać jako
|
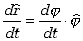
|
(2.21) |
Wektor prędkości wyrażony we współrzędnych biegunowych ma więc postać
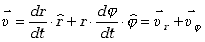
| (2.22)
|
W ten sposób rozłożyliśmy wektor prędkości w układzie biegunowym na dwie składowe
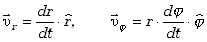
| (2.23)
|
Pierwsza nosi nazwę prędkości radialnej,
jest bowiem skierowana wzdłuż promienia wodzącego.
Druga, o kierunku do niej prostopadłym, nazywa się
prędkością transwersalną lub azymutalną.
|
Wartość bezwzględną wektora prędkości wyrażona przez jej składowe w układzie
biegunowym ma postać: |
|
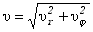
|
(2.24) |
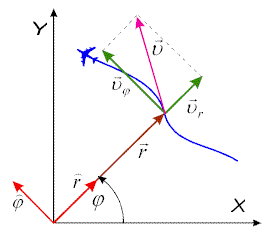
| Rysunek obok ilustruje relacje pomiędzy
składowymi prędkości w układzie biegunowym. Kolorem niebieskim
pokazany jest przykładowy tor samolotu, kolorem czerwonym - wersory, brązowym
- promień wodzący, różowym- wektor prędkości i zielonym - jego składowe
w układzie biegunowym. |
|
Rys.2.6. Składowe: radialna i transwersalna wektora prędkości.
|
|


