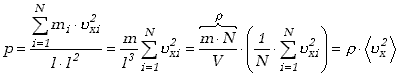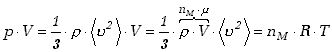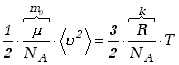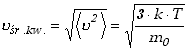Mikroskopowy opis ciśnienia i temperatury
Ciśnienie
 |
Czym jest ciśnienie gazu z mikroskopowego
punktu widzenia?
Ścianki naczynia zawierającego pewną porcję gazu uderzane są
ustawicznie przez cząsteczki będące w chaotycznym ruchu. Wyznaczmy
przekaz pędu przy takich zderzeniach. Dla uproszczenia przyjmijmy, że
naczynie ma kształt sześcianu o długości ścianek równej 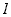 . .
|
| Rys. 12.1. Cząsteczki gazu w sześciennym
naczyniu. |
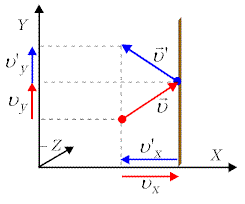
Prędkość cząsteczki w układzie współrzędnych prostokątnych zapiszemy
w postaci
|
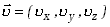
|
(12.1) |
Pęd przekazany ściance będzie odwrotnego znaku, a więc wyniesie 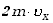 .Czas
przelotu cząsteczki przez kostkę wynosi
.Czas
przelotu cząsteczki przez kostkę wynosi 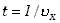 zaś przelot w obie strony trwać będzie dwa razy dłużej;
zaś przelot w obie strony trwać będzie dwa razy dłużej; 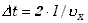 .
Częstość
.
Częstość 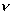 uderzeń
o ściankę, czyli liczba uderzeń w jednostce czasu będzie odwrotnością
czasu przelotu cząsteczki w dwie strony czyli
uderzeń
o ściankę, czyli liczba uderzeń w jednostce czasu będzie odwrotnością
czasu przelotu cząsteczki w dwie strony czyli 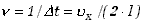 .
Pęd przekazany ściance w jednostce czasu równy będzie pędowi przekazanemu w
jednym uderzeniu pomnożonemu przez liczbę uderzeń w jednostce czasu.
.
Pęd przekazany ściance w jednostce czasu równy będzie pędowi przekazanemu w
jednym uderzeniu pomnożonemu przez liczbę uderzeń w jednostce czasu.
|
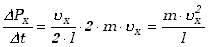
|
(12.4) |
Z drugiej zasady dynamiki wiemy, że 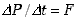 .
Pamiętamy też, że ciśnienie jest stosunkiem siły do powierzchni, na którą
siła działa . Powierzchnia ta jest w naszym przypadku równa kwadratowi długości
ścianki. Ciśnienie będące skutkiem uderzeń jednej cząsteczki w ściankę
wynosi więc
.
Pamiętamy też, że ciśnienie jest stosunkiem siły do powierzchni, na którą
siła działa . Powierzchnia ta jest w naszym przypadku równa kwadratowi długości
ścianki. Ciśnienie będące skutkiem uderzeń jednej cząsteczki w ściankę
wynosi więc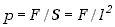 .
Sumując przyczynki od wszystkich uderzających w ściankę cząsteczek i dzieląc
przez jej powierzchnię otrzymujemy wyrażenie na ciśnienie gazu działające
na ściankę
.
Sumując przyczynki od wszystkich uderzających w ściankę cząsteczek i dzieląc
przez jej powierzchnię otrzymujemy wyrażenie na ciśnienie gazu działające
na ściankę
|
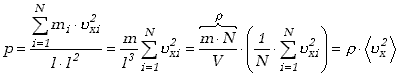
|
(12.5) |
Założyliśmy tu, że wszystkie cząsteczki mają tę samą masę 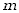 .
Długość ścianki w trzeciej potędze zamieniliśmy objętością sześcianu
.
Długość ścianki w trzeciej potędze zamieniliśmy objętością sześcianu 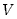 .
Iloczyn masy cząsteczki przez liczbę cząsteczek jest masą gazu w naczyniu,
zaś podzielony przez objętość jest gęstością gazu, którą oznaczyliśmy
symbolem
.
Iloczyn masy cząsteczki przez liczbę cząsteczek jest masą gazu w naczyniu,
zaś podzielony przez objętość jest gęstością gazu, którą oznaczyliśmy
symbolem 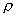 . Symbol
. Symbol 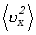 oznacza
wartość średnią kwadratu składowej wektora prędkości wzdłuż osi
oznacza
wartość średnią kwadratu składowej wektora prędkości wzdłuż osi 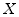 .
.
Biorąc pod uwagę, że kwadrat wektora równy jest sumie kwadratów jego składowych
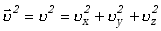 i pamiętając, że
wszystkie kierunki wektora prędkości są tak samo prawdopodobne oraz, że
ruchy w każdym kierunku są niezależne - możemy
zamienić wartość średnią kwadratu składowej przez wartość średnią
kwadratu wektora prędkości, czyli
i pamiętając, że
wszystkie kierunki wektora prędkości są tak samo prawdopodobne oraz, że
ruchy w każdym kierunku są niezależne - możemy
zamienić wartość średnią kwadratu składowej przez wartość średnią
kwadratu wektora prędkości, czyli
|
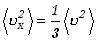
|
(12.6) |
Ostatecznie otrzymujemy wzór wyrażający związek pomiędzy mikroskopowymi
(średnia prędkość cząsteczek) i makroskopowymi (ciśnienie i gęstość) własnościami
gazu
|
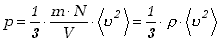
|
(12.7) |
W naszych rozważaniach nie uwzględnialiśmy zderzeń pomiędzy cząsteczkami.
Zwróćmy jednak uwagę, że w zderzeniach sprężystych jest zachowany pęd
oraz energia kinetyczna, a więc zderzenia te nie będą wpływać na wartość
średnią pędu przekazywanego ściankom naczynia. Wybraliśmy także
regularny (sześcienny) kształt naczynia. W warunkach równowagi ciśnienie
wywierane na wszystkie ścianki o dowolnym kształcie a także wewnątrz
naczynia jest jednakowe, o czym wiemy z prawa Pascala. Rozważania nasze mają
więc ogólny charakter.
Temperatura
Dla znalezienia związku pomiędzy makroskopową i mikroskopową interpretacją
temperatury pomnóżmy lewą i prawą stronę równania (12.7) przez objętość
naczynia 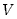 i porównajmy
to z równaniem stanu gazu doskonałego
i porównajmy
to z równaniem stanu gazu doskonałego
|
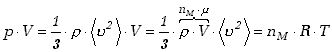
|
(12.8) |
We wzorze tym iloczyn gęstości i objętości jest po prostu masą gazu, którą
następnie wyraziliśmy w molach oznaczając przez 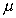 jego masę molową.
jego masę molową.
Mnożąc stronami przez 3/2 i dzieląc przez liczbę Avogadro
otrzymujemy
|
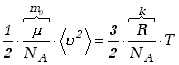
|
(12.9) |
Zauważamy przy tym, że masa molowa podzielona przez liczbę Avogadro to po
prostu masa jednej cząsteczki 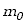 . Iloraz stałej
gazowej i liczby Avogadro, to stała Boltzmanna
. Iloraz stałej
gazowej i liczby Avogadro, to stała Boltzmanna 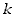 ,
którą wprowadziliśmy wzorem (11.14). Stała ta ma sens stałej gazowej
odniesionej do jednej cząsteczki. Jak zobaczymy, stała ta odgrywa
fundamentalna rolę w fizyce.
,
którą wprowadziliśmy wzorem (11.14). Stała ta ma sens stałej gazowej
odniesionej do jednej cząsteczki. Jak zobaczymy, stała ta odgrywa
fundamentalna rolę w fizyce.
Wykorzystując wprowadzone oznaczenia możemy przepisać równanie (12.9) w
postaci
|

|
(12.10) |
Wyrażenie po lewej stronie jest wielkością mikroskopową - średnią
energią kinetyczną chaotycznego ruchu cząsteczek gazu, wyrażenie po prawej
stronie jest proporcjonalne do wielkości makroskopowej - temperatury
bezwzględnej ciała. Stwierdzamy więc że,
temperatura jest miarą średniej energii kinetycznej
chaotycznego ruchu cząsteczek.
Średnia wartość kwadratu prędkości wynosi
|
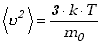 . .
|
(12.10a) |
Na tej podstawie możemy określić tzw. średnią prędkość kwadratową
definiując ją jako
|
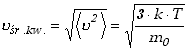
|
(12.10b) |
Zasada ekwipartycji energii
W naszych rozważaniach uwzględnialiśmy tylko energię ruchu postępowego
cząsteczek. Jest to wystarczające jeżeli rozpatrujemy gaz jednoatomowy -
kiedy atomy możemy traktować jako punkty materialne. Do opisu ich położenia
wystarczy podanie trzech współrzędnych. Cząsteczki wieloatomowe mogą
wykonywać także ruch obrotowy wokół swego środka ciężkości; możliwe
są również drgania atomów wchodzących w skład cząsteczki. Z ruchami tymi
także wiąże się pewna energia (z obrotem - energia kinetyczna ruchu
obrotowego, z drganiami - energia kinetyczna i energia potencjalna).
Położenie punktu materialnego w przestrzeni jest w pełni opisane przez
trzy współrzędne. Dwa połączone na sztywno punkty materialne mogą być
opisane za pomocą pięciu (a nie sześciu ) liczb, bowiem fakt ich sztywnego połączenia
sprawia, że do opisu ich położenia wystarczy podać położenie jednego z
nich oraz dwa kąty określające orientację w przestrzeni prostej łączącej
te punkty. Położenie drugiego punktu na tej prostej jest znane, skoro znana
jest ich wzajemna odległość. Położenie N niezależnych punktów
materialnych wymaga jednak 3N liczb, skoro traktujemy te punkty za niezależne.
Położenie ciała sztywnego wymaga podania sześciu liczb. Pięć z nich określa,
podobnie jak w przypadku układu dwóch ciał, położenie wybranego punktu, na
przykład środka ciężkości, oraz kierunek wybranej prostej, na przykład osi
obrotu. Punkty nie będące na osi mogą jednak zmieniać swe położenie
wskutek ruch obrotowego wokół osi, potrzeba wiec jeszcze znać kąt obrotu -
razem sześć liczb.
Liczbę niezależnych wielkości za pomocą których może być opisane położenie
układu nazywamy liczbą stopni swobody układu.
Liczba ta określa więc możliwości ruchów jakie może wykonywać cząsteczka.
Z każdym ruchem wiąże się określona energia. Jeżeli ruch jest całkowicie
chaotyczny i żaden rodzaj ruchu nie jest uprzywilejowany, to można przyjąć,
że na każdy stopień swobody przypada jednakowa porcja energii. Stwierdzenie
to jest treścią zasady ekwipartycji energii.
Zasada ekwipartycji energii
Na każdy stopień swobody cząsteczki przypada średnio
ta sama energia.
Jej wartość możemy określić na przykładzie ruchu postępowego cząsteczek
punktowych. W tym przypadku liczba stopni swobody wynosi 3, a średnia energia
kinetyczna cząsteczki, zgodnie z wzorem (12.10), jest równa 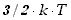 .
Możemy więc uzupełnić ilościowo treść zasady ekwipartycji energii.
.
Możemy więc uzupełnić ilościowo treść zasady ekwipartycji energii.
Na każdy stopień swobody cząsteczki przypada średnio
energia równa kT/2 .
W oparciu o nasze rozważania widzimy, że energia ruchu cząsteczek w gazach
wieloatomowych jest większa niż w gazach jednoatomowych.
Średnia energia cząsteczki o danej liczbie stopni swobody f
wynosi więc 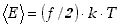 . Dla
jednego mola gazu doskonałego, kiedy zaniedbuje się energię potencjalną
wynikającą z sił wzajemnego oddziaływania cząsteczek, iloczyn
. Dla
jednego mola gazu doskonałego, kiedy zaniedbuje się energię potencjalną
wynikającą z sił wzajemnego oddziaływania cząsteczek, iloczyn 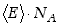 jest po prostu energią wewnętrzną gazu równą
jest po prostu energią wewnętrzną gazu równą 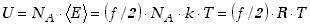 .
.

![]() .
.