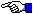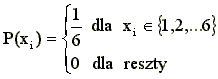
1. Krótki wstęp do rachunku
prawdopodobieństwa.
Podstawowym pojęciem rachunku prawdopodobieństwa jest prawdopodobieństwo P(xi) wystąpienia jakiegoś zdarzenia xi. Prawdopodobieństwo może przyjmować wartości z przedziału <0,1>. Przy czym jeśli jest równe 1 to zdarzenie na pewno nastąpi, jeśli zaś jest przyjmuje wartość 0 to zdarzenie nigdy nie nastąpi. Dla przykładu, przy rzucie kostką do gry, wyrzucenie w jednym rzucie pewnej konkretnej całkowitej liczby z przedziału <1,6> wynosi 1/6. Jeżeli interesuje nas zdarzenie polegające na wyrzucenie dowolnej liczby całkowitej z tego przedziału, to jego prawdopodobieństwo jest równe 1. Natomiast otrzymanie liczby spoza tego przedziału nigdy nie nastąpi więc prawdopodobieństwo wynosi 0.
Innym pojęciem rachunku prawdopodobieństwa jest rozkład prawdopodobieństwa. Jest to funkcja której wartościami są prawdopodobieństwa zdarzeń, zaś zbiór argumentów stanowią wszystkie możliwe zdarzenia.
I tak na przykład dla naszej gry w kości rozkład prawdopodobieństwa zdarzeń będących wynikami jednego rzutu ma postać:
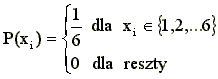
Do tej pory rozważaliśmy jedynie zdarzenia których liczba jest skończona, możliwe są jednak sytuacje kiedy liczba możliwych zdarzeń jest nieprzeliczalna (np. przy pomiarze współrzędnych danego obiektu możemy uzyskać dowolne ich wartości nawet przy założeniu, że mogą być one jedynie w skończonym przedziale). Takie zdarzenia nazywamy zmiennymi losowymi ciągłymi, w odróżnieniu od zdarzeń wcześniejszego typu, zwanych zmiennymi losowymi dyskretnymi.
Dla zmiennych losowych ciągłych nie zajmujemy się prawdopodobieństwem wystąpienia jakiejś konkretnej wartość (jest ono równe 0) ale prawdopodobieństwem że wartość ta zawiera się w jakimś przedziale (a,b) . Prawdopodobieństwo to definiujemy następująco:
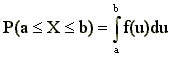
gdzie: X wartość zmiennej losowej, f(u) - funkcja gęstości prawdopodobieństwa.
Funkcja f(u) ma następujący sens: prawdopodobieństwo że wartość zmiennej losowej jest w przedziale o nieskończenie małej długości du wynosi f(u)du.
Dla zmiennych losowych typu ciągłego rozkład prawdopodobieństwa to postać funkcji gęstości dla wszystkich zdarzeń. Na przykład rozkład prawdopodobieństwa zmiennej losowej będącej położeniem cząsteczki w jakieś pojemniku o objętości V wynosi:
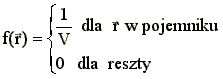
Wielkościami charakteryzującymi dany rozkład prawdopodobieństwa są tak zwane momenty.
Momentem pierwszego rządu nazywamy wielkość:
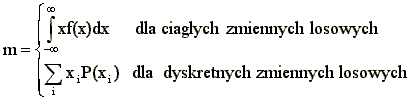
Nosi on także nazwy średniej lub wartości przeciętnej ponieważ m jest odpowiednikiem środka ciężkości, gdyby prawdopodobieństwo traktować jako masy.
Obok średniej drugim ważnym momentem jest moment drugiego rzędu mający postać:
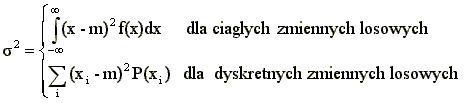
Dokładnie rzecz ujmując jest to jeden z momentów centralnych. Nazywany jest on także wariancją zmiennej losowej. Jego pierwiastek nosi nazwę odchylenia standardowego
i jest miarą tego jak zmienne losowe (opisane jakimśrozkładem prawdopodobieństwa) są rozrzucone względem średniej. Stosują analogię do masy wariancja
2 jest odpowiednikiem momentem bezwładności względem środka ciężkości.