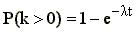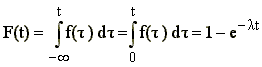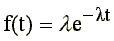Do tej pory interesowało nas jedynie ile było intersujących nas zdarzeń w pewnym, określonym odcinku czasu. Jednak z właściwości rozkładu Poisson można ustalić rozkład czasu oczekiwania na zdarzenie.
Z niezależności statystycznej między poszczególnymi zdarzeniami wynika, że nie ważne jest którą chwilę czasu rozpatrujemy. Statystyczne własności badanego zjawiska będą identyczne w każdym momencie pomiarów. Wynika z tego więc, że zamiast rozpatrywać prawdopodobieństwo pojawienia sie jakiegoś zdarzenia w przedziale (t₁,t₂), można rozpatrywać prawdopobieństwo rejestracji w przedziale (0,t₂-t₁).

Załóżmy, że inetresuje nas prawdopdobieństwo nie zarejestrowania w od czasu 0 do czasu t ani jednego zdarzenia. Z rozkładu Poissona wynosi ono:

                      

Oczywiście prawdopodobieństwo rejestracji  jakiej kolwiek liczby zdarzeń wynosi:
                      

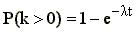
Ponieważ nie istnieją czasy ujemne to wielkość ta jest  równa również dystrybuancie F(t) czasu pojawienia się sygnału.

Z tego zaś bezpośrednio po przez całkowanie F(t) po czasie możemy uzyskać gęstość rozkładu czasu oczekiwania na sygnał. Wynosi ona.

                 
Jest to dobrze znany razkład wykładniczy.

Wiadomo, że dla rozkładu wykładniczego średnia wynosi 1/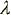 i jest równa odchyleniu standardowemu . Co z tego wynika. Mianowicie to, że jeżeli rejestrujemy np. jakieś cząstki z częstotliwością jedna na godzinę. To bardzo często nie zarejestrujemy żadnej przez wiele godzin.

---

Spis treści