4. Przypadek zmiennej w czasie intensywności.

Rozkład Poissona omówiony w poprzednich punktach, opisywał prawdopodobieństwo zarejestrowania pewnej liczby cząstek w czasie t.

Wyprowadzając go założyliśmy nie wspominając o tym, że w całej serii n pomiarów tj. w czasie nt intensywność promieniowania (np. pochodzenia kosmicznego lub z rozpadów promieniotwórczych) jest niezmienna. Jeżeli wielkość ta jest funkcją czasu,  co ma miejsce, na przykładu, jeżeli wykonujemy pomiary strumienia cząstek z akceleratorów impulsowych, lub czas pomiarów liczby rozpadów jest na tyle długi, że jest porównywalny z czasem połowicznego rozpadu jąder źródła.

Ponieważ jednak wielkość lt pełni przy wyprowadzaniu rozkładu Poissona jedynie rolę mnożnika, to możemy ją uogólnić nadając jej postać.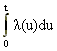

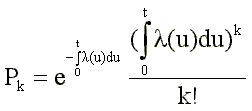
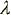Teraz rozkładu Poissona możemy zapisać następująco:

Ten rozkład  zachowuje swoje poprzednie własności tylko wtedy, kiedy (t) jest funkcją okresową.