Widać, że średnia
m jest proporcjonalna do czasu obserwacji. Jest oczywiste, gdyż im dłużej
będziemy zliczać tym większe liczby będziemy otrzymywać. Ponadto średnia
jest również proporcjonalna do 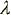 . Parametr ten ma sens
intensywności promieniowania tzn, średniej liczby cząsteczek przechodzących przez detektor w ciągu jednej sekundy.
. Parametr ten ma sens
intensywności promieniowania tzn, średniej liczby cząsteczek przechodzących przez detektor w ciągu jednej sekundy.
Wraz ze wzrostem wartości średniej liczby zliczeń m następuje wzrost odchylenia standardowego 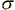 równego
równego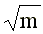 . Znaczy to, że mierzone liczby cząstek będą coraz bardziej rozrzucone w stosunku do średniej.
. Znaczy to, że mierzone liczby cząstek będą coraz bardziej rozrzucone w stosunku do średniej.
Na znajdującym się niżej rysunku widać zmiany rozkładu wraz ze zmianą średniej m
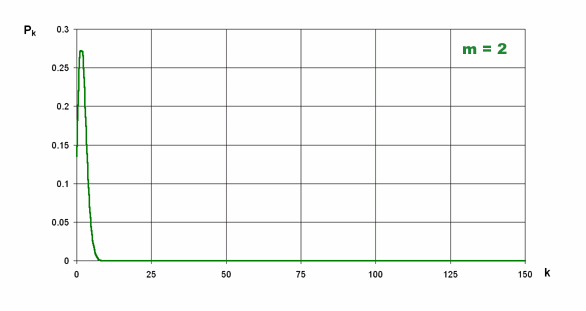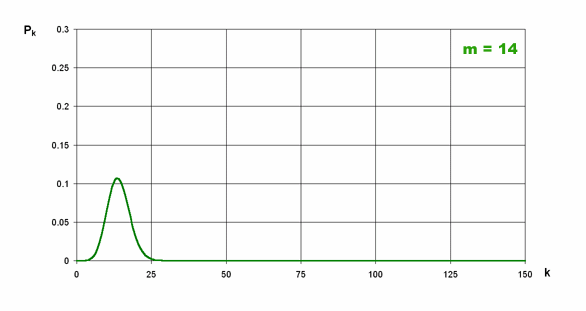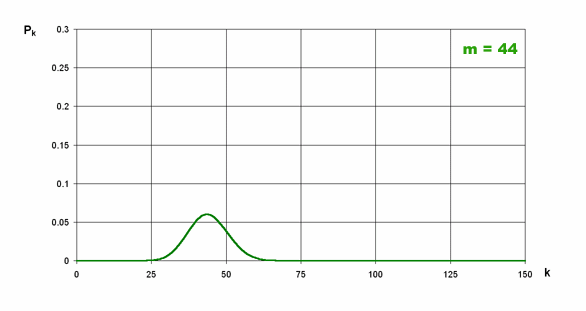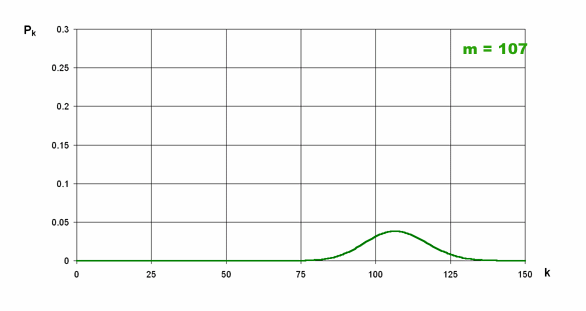
Rysunek: Zależność "kształtu" rozkładu od średniej m
Fakt że średnia i wariancja są sobie równe ma większy sens. Wynika
z niego bowiem, że do określenia rozkładu Poissona wystarczy znać tylko jedną
z tych wielkości. Jest to rozkład jednoparametrowy.
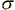 2 są równe i wynoszą
2 są równe i wynoszą 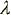 t.
t.![]() (odchylenie standardowe
(odchylenie standardowe 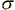 ).
).