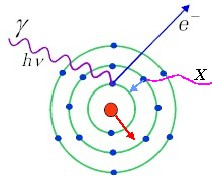
Rys.1.3.1
Zjawisko fotoelektryczne
![]()
(1.3.1)
W wyniku zajścia tego procesu foton znika, atom zostaje zjonizowany, a wyemitowany elektron ma energię (porównaj wzór (2.3.2)):
| Efekty wywoływane przez fotony w materii |
Fotony - kwanty promieniowania elektromagnetycznego - oddziaływają z materią na wiele sposobów. Trzy z nich odgrywają zasadniczą rolę: zjawisko fotoelektryczne, efekt Comptona i produkcja par elektron-pozyton. Dwa pierwsze z nich już rozpatrywaliśmy omawiając, kwantowe cechy promieniowania elektromagnetycznego, trzeci proces omówimy poniżej.
Teraz skupimy uwagę na tych cechach oddziaływania fotonów z materią, które dotyczą przekazu energii i absorpcji promieniowania. Każdy z procesów reprezentowany jest symbolicznym rysunkiem. (Pamiętajmy jednak, że rysunki te nie odzwierciedlają bynajmniej relacji geometrycznych czy kinematycznych, ale maja za zadanie zilustrować poglądowo mechanizm zachodzenia poszczególnych procesów.) Prawdopodobieństwa ich zachodzenia zależne są od energii fotonów oraz własności materiału absorbenta.

Rys.1.3.1 |
Zjawisko fotoelektryczne, czyli pochłonięcie fotonu przez atom i emisja elektronu z powłoki leżącej w pobliżu jądra, tj. | |
|
|
(1.3.1) |
|
|
W wyniku zajścia tego procesu foton znika, atom zostaje zjonizowany, a wyemitowany elektron ma energię (porównaj wzór (2.3.2)): |
||
|
|
(1.3.2) | |
| gdzie W jest tzw. pracą wyjścia odpowiadającą energii wiązania elektronu na orbicie atomowej. | ||
Zjawisko fotoelektryczne zachodzić może wyłącznie dla elektronów związanych w atomach. Kinematyka wymaga, by cześć pędu fotonu przejęło trzecie ciało jakim jest jądro atomowe. Właśnie dlatego efekt fotoelektryczny zachodzi najczęściej dla elektronów znajdujących się na powłokach będących najbliżej jądra, chociaż z tym właśnie wiąże się też warunek wyrażony wzorem (2.3.4) określający minimalną energię fotonu przy której może zajść zjawisko fotoelektryczne. Najsilniej związane są elektrony na powłoce najbliższej jądru zwanej powłoką K. Dlatego energię fotonu umożliwiającą uwolnienie elektronu z tej powłoki nazywa się często krawędzią K.
Po uwolnieniu elektronu z powłoki w pobliżu jądra może nastąpić przeskok na tę powłokę elektronu z powłoki dalszej. Wyzwalana przy tym energia emitowana jest w postaci kwantu promieniowania elektromagnetycznego w zakresie rentgenowskim. Może też nastąpić przekazanie energii innemu elektronowi w atomie i jego emisja. Elektron taki nazywany jest elektronem Auger'a.
Przekrój czynny na zjawisko fotoelektryczne rośnie bardzo szybko ze wzrostem liczby atomowej materiału w którym efekt zachodzi oraz maleje ze wzrostem energii samego fotonu. Można to zapisać w postaci empirycznej zależności
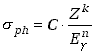 |
(1.3.3) |
gdzie Z jest liczbą atomową materiału (absorbenta),
a ![]() jest energią fotonu. Dla niskich energii
(
jest energią fotonu. Dla niskich energii
(![]() )
wartości wykładników
potęg we wzorze (1.3.3) są: k=4.0, n=3.5;
dla energii bardzo wysokich
(
)
wartości wykładników
potęg we wzorze (1.3.3) są: k=4.0, n=3.5;
dla energii bardzo wysokich
(![]() )
k=4.6, n=1.0; C jest stałym,
tj niezależnym od Z i
)
k=4.6, n=1.0; C jest stałym,
tj niezależnym od Z i
![]() ,współczynnikiem
proporcjonalności.
,współczynnikiem
proporcjonalności.
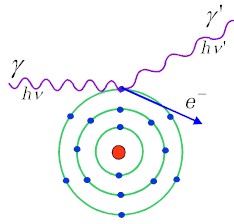 Rys.1.3.2 Efekt Comptona |
Efekt Comptona, czyli rozproszenie fotonu na quasi-swobodnym elektronie. | |
|
|
(1.3.4) |
|
|
W rezultacie zajścia tego procesu foton zostaje rozproszony, a energia rozproszonego fotonu jest (oczywiście) mniejsza od energii fotonu pierwotnego. Jak już pokazaliśmy omawiając kinematyczne zależności w efekcie Comptona, energia rozproszonego fotonu jest też zależna od kąta rozproszenia. (2.4.17)) |
||
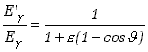 |
(1.3.5) | |
|
gdzie
|
||
Jak widać z postaci tego wzoru stosunek energii fotonu rozproszonego
do energii fotonu pierwotnego ma najmniejszą wartość dla
rozproszenia do tyłu,
![]() i zależny jest, poprzez wartość
i zależny jest, poprzez wartość
![]() ,
od energii fotonu. Najsilniejsza zależność od kąta jest dla dużych energii.
,
od energii fotonu. Najsilniejsza zależność od kąta jest dla dużych energii.
Przekrój czynny na efekt Comptona określa wzór Kleina Nishiny, który ma złożoną formę. Dla dużych energii fotonów przekrój czynny na jeden elektron może być wyrażony prostą zależnością
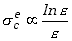 , , |
(1.3.6) |
z której widać, że przekrój czynny na efekt Comptona jest
malejącą funkcją energii pierwotnego fotonu. W atomie, gdzie jest Z
elektronów, przekrój czynny na jeden atom jest większy i określony jest zależnością:
![]() .
.
Zauważmy, że w przypadku efektu Comptona tylko część energii fotonu przekazana
jest elektronowi; pozostałą unosi foton
rozproszony. Przekrój czynny na efekt Comptona rozkładamy dlatego na dwa
składniki: przekrój czynny na rozpraszanie
![]() oraz przekrój czynny na absorpcję,
oraz przekrój czynny na absorpcję,
![]() .
Relację pomiędzy
przekrojem czynnym na efekt Comptona, dany wzorem (1.3.6) a jego składowymi
przekrojami czynnymi można wyrazić w postaci
.
Relację pomiędzy
przekrojem czynnym na efekt Comptona, dany wzorem (1.3.6) a jego składowymi
przekrojami czynnymi można wyrazić w postaci
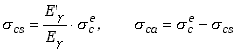 |
(1.3.7) |
|
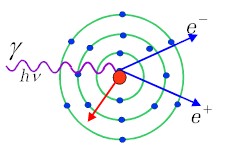
Zjawisko tworzenia par elektron-pozyton
polega na zamianie (konwersji) fotonu w parę: pozyton i
elektron, tj. |
|
| Rys.1.3.3 Tworzenie par
|
|
(1.3.8) |
gdzie (A,Z) oznacza jądro o liczbie masowej A i atomowej Z.
Ze spełnienia praw zachowania
wynika relacja określająca energię progową fotonu powyżej której
może zachodzić zjawisko tworzenia par
![]()
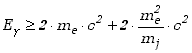 |
(1.3.9) |
gdzie ![]() jest energią fotonu,
jest energią fotonu, ![]() jest masą elektronu a
jest masą elektronu a ![]() masą jądra;
masą jądra; ![]() -
jest (oczywiście) prędkością światła. Ponieważ masa jądra jest tysiące razy większa niż
masa elektronu, drugi człon we wzorze (1.3.1) można zwykle zaniedbać wyrażając energię progową prostszym wzorem
-
jest (oczywiście) prędkością światła. Ponieważ masa jądra jest tysiące razy większa niż
masa elektronu, drugi człon we wzorze (1.3.1) można zwykle zaniedbać wyrażając energię progową prostszym wzorem
|
|
(1.3.10a) |
Oznacza to, że energia fotonu musi byś większa od energii odpowiadającej sumie mas pozytonu i elektronu, które to cząstki tworzone są w procesie konwersji.
Kiedy proces produkcji par zachodzi w polu elektrostatycznym elektronu, to energia progowa zgodnie ze wzorem (1.3.9), gdzie zamiast masy jądra wstawiamy masę elektronu, jest większa i wynosi
|
|
(1.3.10b) |
Proces ten jest jednak znacznie mniej prawdopodobny niż konwersja w polu jądra.
Procesem odwrotnym do tworzenia par
![]() jest proces anihilacji pozytonu z elektronem, w którym para pozyton-elektron
zamienia się na dwa fotony, tj. na dwa kwanty
promieniowania elektromagnetycznego.
jest proces anihilacji pozytonu z elektronem, w którym para pozyton-elektron
zamienia się na dwa fotony, tj. na dwa kwanty
promieniowania elektromagnetycznego.
Przekrój czynny na wytworzenie pary
![]() przez foton o energii
przez foton o energii ![]() ,
w sąsiedztwie jądra o liczbie atomowej
Z może być przedstawiony przybliżonym wzorem postaci
,
w sąsiedztwie jądra o liczbie atomowej
Z może być przedstawiony przybliżonym wzorem postaci
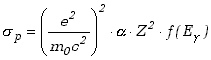 |
(1.3.11) |
gdzie ![]() ,
a
,
a ![]() rośnie logarytmiczne z energią fotonu, a przy energiach bardzo dużych przestaje
zależeć od energii.
rośnie logarytmiczne z energią fotonu, a przy energiach bardzo dużych przestaje
zależeć od energii.
Współczynnik osłabienia wiązki i współczynnik pochłaniania (absorpcji)
Zauważmy, że wyeliminowanie fotonu z wiązki nie oznacza, że cała jego
energia została zaabsorbowana w materiale. Zaabsorbowana
energia, to energia kinetyczna elektronów, które zostały uwolnione, bądź
wyprodukowane w procesie oddziaływania fotonu z materią. W
zjawisku fotoelektrycznym i procesie tworzenia par foton pierwotny znika
i cała jego energia przekazywana jest naładowanym elektrycznie
produktom wtórnym. Ich sumaryczna energia kinetyczna jest nieco mniejsza
niż energia pierwotnego fotonu, bo w zjawisku fotoelektrycznym
jego energia zużywana jest też na pracę wyjścia a w procesie tworzenia
par na wyprodukowania pary
![]() .
Zasadniczo odmienna jest sytuacja w przypadku efektu Comptona, gdzie tylko
cześć energii fotonu pierwotnego przejmuje elektron w postaci
swej energii kinetycznej. Znaczna cześć energii jest
unoszona przez foton wtórny.
.
Zasadniczo odmienna jest sytuacja w przypadku efektu Comptona, gdzie tylko
cześć energii fotonu pierwotnego przejmuje elektron w postaci
swej energii kinetycznej. Znaczna cześć energii jest
unoszona przez foton wtórny.
W konsekwencji tych wszystkich zależności - przekrój czynny,
a więc i współczynnik osłabienia wiązki fotonów
![]() ,
zależy w złożony
sposób zarówno od energii fotonów jak i od liczby atomowej
Z materiału absorbenta. Oznaczając przez
,
zależy w złożony
sposób zarówno od energii fotonów jak i od liczby atomowej
Z materiału absorbenta. Oznaczając przez
![]() współczynnik osłabienia
wiązki związany ze zjawiskiem fotoelektrycznym, przez
współczynnik osłabienia
wiązki związany ze zjawiskiem fotoelektrycznym, przez
![]() - związany
z efektem Comptona, a przez
- związany
z efektem Comptona, a przez
![]() -
z tworzeniem par oraz przez
-
z tworzeniem par oraz przez
![]() i
i ![]() współczynniki rozpraszania i absorpcji w efekcie Comptona mamy relację
współczynniki rozpraszania i absorpcji w efekcie Comptona mamy relację
|
|
(1.3.12 |
Wprowadzając współczynnik pochłaniania (absorpcji) promieniowania gamma
w materiale ![]() ,
możemy sformułować zależność
,
możemy sformułować zależność
|
|
(1.3.13) |
gdzie czynniki f oznaczają część energii fotonów zaabsorbowaną w materiale wskutek zajścia poszczególnych procesów.
Dla zjawiska fotoelektrycznego mamy na podstawie wzoru (2.3.2)
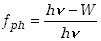 |
(1.3.14) |
Czynnik ten jest bliski jedności, kiedy energia fotonów jest znacznie większa niż praca wyjścia, a tak jest zwykle w przypadku fotonów emitowanych w przemianach jądrowych.
W zjawisku Comptona podział energii pomiędzy foton i elektron zależny jest od kąta rozproszenia, wzór (1.3.5), zaś zależności ta jest funkcją energii fotonu pierwotnego.
W przypadku kreacji par
![]() mamy zależność
mamy zależność
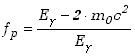 |
(1.3.15) |
Dla energii fotonów znacznie większej od energii spoczynkowej elektronu czynnik ten bliski jest jedności.
| Rysunek 1.3.6 ilustruje poglądowo obszary dominacji poszczególnych efektów w funkcji zarówno energii fotonów, jak i liczby atomowej Z. Obszar dominacji efektu fotoelektrycznego obejmuje najniższe energie ale sięga tym wyższych wartości, im większa jest liczba atomowa (ładunek jądra atomowego) danego materiału. Efekt Comptona dominuje w obszarze energii wokół wartości 1MeV i dlatego właśnie w tym obszarze mamy dużą różnicę pomiędzy współczynnikiem osłabienia wiązki i współczynnikiem absorpcji. Efekt kreacji par pojawia się dla energii powyżej 1MeV i dominuje wcześniej dla pierwiastków ciężkich. | |
| Rys. 1.3.6. Obszary dominacji różnych efektów oddziaływania fotonów z materią w funkcji energii fotonów i liczby atomowej absorbenta Z. |
Co oznaczają w praktyce konkretne wartości współczynników osłabienia wiązki
i absorpcji? Fotografia 1.3.7. pokazuje "żywy" przykład oddziaływania
promieniowania gamma z materią. Z lewej strony widać ślad cząstki
wyemitowanej z punktu w który celują też dwa pęki innych śladów rozciągających
się wzdłuż całej fotografii. Te pęki, które stanowią rezultat kreacji dwóch
par ![]() mają swój początek w pewnej odległości od punktu, w który celują. Fotony
przebiegły pewien odcinek bez oddziaływania, a następnie miała miejsce
konwersja. Wyprodukowane dwa elektrony i dwa pozytony pozostawiły ślady w
komorze pęcherzykowej dając początek tzw. kaskadom elektronowo-fotonowym..
Wszystkie ślady powstały wskutek procesów jonizacji, tj. wydzielenia energii.
Trzeba zdawać sobie sprawę, że takie procesy zachodzą również wskutek
promieniowania kosmicznego, a kaskady podobne tym na zdjęciu rozwijają się
także i w nas. Nie jest to jednak powód do obaw, bo procesy takie zachodziły
też w czasach dawnych, a ludzkość przetrwała jednak do chwili obecnej. Więcej
o kaskadach elektronowo-fotonowych powiemy omawiając oddziaływania elektronów
z materią.
mają swój początek w pewnej odległości od punktu, w który celują. Fotony
przebiegły pewien odcinek bez oddziaływania, a następnie miała miejsce
konwersja. Wyprodukowane dwa elektrony i dwa pozytony pozostawiły ślady w
komorze pęcherzykowej dając początek tzw. kaskadom elektronowo-fotonowym..
Wszystkie ślady powstały wskutek procesów jonizacji, tj. wydzielenia energii.
Trzeba zdawać sobie sprawę, że takie procesy zachodzą również wskutek
promieniowania kosmicznego, a kaskady podobne tym na zdjęciu rozwijają się
także i w nas. Nie jest to jednak powód do obaw, bo procesy takie zachodziły
też w czasach dawnych, a ludzkość przetrwała jednak do chwili obecnej. Więcej
o kaskadach elektronowo-fotonowych powiemy omawiając oddziaływania elektronów
z materią.
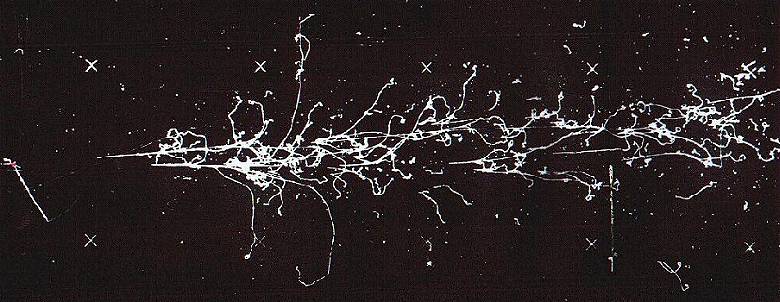 |
| Fot.1.3.7. Kaskady elektronowo-fotonowe zarejestrowane w komorze pęcherzykowej wypełnionej ciekłym ksenonem. |
Zwróćmy jeszcze uwagę na statystyczny charakter oddziaływania fotonów z materią.