Wiemy już, że cząstkom możemy przypisać fale, których częstotliwość i długość określają wzory (12.1.1) i (12.1.2). Pamiętamy też z kursu Fizyka I, że ruch wszelkich obiektów makroskopowych w nierelatywistycznej mechanice klasycznej opisują równania Newtona. Nasuwa się wiec naturalne pytanie - czy można sformułować równania, które opisywałyby ruch obiektów mikroskopowych i w których uwzględniona byłaby ich dwoista, falowo-korpuskularna natura.
Spróbujmy przypisać poruszającej się swobodnie cząstce falę o określonej
częstotliwości i długości oraz postarajmy się sformułować równanie,
którego rozwiązaniem będzie funkcja opisująca przemieszczanie się tej fali.
Funkcję taką nazywać będziemy funkcją falową i
oznaczać będziemy symbolem ![]() .
.
Zapiszmy funkcję falową cząstki swobodnej w postaci
| (12.3.1) |
gdzie ![]() jest jednostką urojoną. Ten zapis funkcji zespolonej w formie wykładniczej równoważny
jest zapisowi w postaci funkcji sinus i cosinus, za
pomocą których opisywaliśmy wcześniej propagację najprostszych fal, tj. płaskich
fal harmonicznych. Wynika to ze związku
pomiędzy dwoma różnymi formami zapisu funkcji zespolonej: trygonometrycznej i
wykładniczej
jest jednostką urojoną. Ten zapis funkcji zespolonej w formie wykładniczej równoważny
jest zapisowi w postaci funkcji sinus i cosinus, za
pomocą których opisywaliśmy wcześniej propagację najprostszych fal, tj. płaskich
fal harmonicznych. Wynika to ze związku
pomiędzy dwoma różnymi formami zapisu funkcji zespolonej: trygonometrycznej i
wykładniczej
| (12.3.2) |
(Zapis liczb zespolonych w postaci wykładniczej i trygonometrycznej omawiany jest szczegółowo w kursie Matematyka I, Lekcja pierwsza; zobacz wzory (1.17) i (1.19)). Formę tę stosuje się również w mechanice klasycznej przyjmując umowę, że rzeczywisty proces propagacji fal reprezentuje część rzeczywista bądź urojona liczby zespolonej. Jak zobaczymy później, w mechanice kwantowej funkcje falowe są funkcjami zespolonymi, bo takie funkcje spełniają równanie którego poszukujemy. Zobaczymy też, że dopiero kwadrat funkcji falowej, który jest liczbą rzeczywistą, reprezentuje wielkości mające interpretację fizyczną.
Podstawiając w wykładniku po prawej stronie wzoru (12.3.1) związki
zdefiniowane wcześniej wzorem (9.1.6): ![]() oraz
oraz
![]() ,
a także te - wynikające z dualizmu korpuskularno-falowego i określone wzorem
(12.1.1):
,
a także te - wynikające z dualizmu korpuskularno-falowego i określone wzorem
(12.1.1): ![]() ,
(12.1.2):
,
(12.1.2):![]() oraz (11.2.11):
oraz (11.2.11): ![]() otrzymujemy zapis funkcji falowej w postaci
otrzymujemy zapis funkcji falowej w postaci
| (12.3.3) |
Podobnie jak przy określaniu postaci równania falowego, będziemy poszukiwać równania różniczkowego, którego rozwiązaniem jest funkcja (12.3.3). W tym celu zróżniczkujmy wyrażenie (12.3.3) względem czasu t, oraz dwukrotnie względem współrzędnej x. Otrzymujemy
| (12.3.4) |
więc wyrażenia na energię i pęd cząstki swobodnej możemy zapisać w postaci
| (12.3.5) |
Pamiętamy z kursu Fizyka I, że energia cząstki swobodnej jest energią kinetyczną E=mv2/2 , a pęd p=mv, więc nierelatywistyczny związek pomiędzy energią kinetyczną cząstki E i jego pędem p jest
| (12.3.6) |
Związek ten zapiszemy wykorzystując przyporządkowania energii i pędu określone wzorem (12.3.5)
| (12.3.7) |
gdzie obie strony pomnożyliśmy przez ![]() .
.
Kiedy ruch odbywa się w polu sił potencjalnych,
to przyrost energii kinetycznej równoważny jest ubytkowi energii potencjalnej,
co wyraża prawo zachowania energii. Dlatego związek pomiędzy energią całkowitą
E oraz energią kinetyczną ![]() i potencjalną V ma wówczas postać
i potencjalną V ma wówczas postać
| (12.3.8) |
Podstawiając znów za E i p wyrażenia określone
wzorem (12.3.5) oraz mnożąc przez ![]() uzyskujemy
równanie
uzyskujemy
równanie
| (12.3.9) |
Równanie tej postaci nosi nazwę równania Schrödingera dla cząstki poruszającej się w jednowymiarowej przestrzeni i czasie, albo jednowymiarowego równania Schrödingera zależnego od czasu.
W tym przypadku funkcja falowa zależy od współrzędnej x i czasu t, czyli
| (12.3.10) |
W przypadku ruchu w przestrzeni trójwymiarowej należy drugą pochodną względem
współrzędnej przestrzennej zastąpić tzw. operatorem Laplace'a działającym
na funkcję falową zależna od trzech współrzędnych i czasu , np. w układzie
współrzędnych prostokątnych ![]() .
Działanie operatora Laplace'a na funkcję daje w wyniku sumę drugich
pochodnych tej funkcji względem współrzędnych
.
Działanie operatora Laplace'a na funkcję daje w wyniku sumę drugich
pochodnych tej funkcji względem współrzędnych
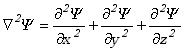 |
(12.3.11) |
Równanie Schrödingera zależne od czasu dla przypadku trójwymiarowego ma więc postać
| (12.3.12) |
Warto zaznaczyć, że związki przedstawione powyżej nie stanowią bynajmniej wyprowadzenia równania Schrödingera, a pokazują raczej, że relacje pomiędzy falowymi i korpuskularnymi własnościami materii mogą byś ujęte w postaci równania różniczkowego na podobieństwo równań Newtona, czy Maxwella. Równanie (12.3.9) i (12.3.12) zostały sformułowane przez Erwina Schrödingera w 1926 roku jako pewien postulat. Równania te opisują zachowanie się obiektów które ujawniają swą korpuskularno- falową naturę, na podobieństwo równań Newtona opisujących ruch ciał makroskopowych w mechanice klasycznej. Zobaczymy jednak, że opis Schrödingera różni się pryncypialnie od opisu Newtona.
Potwierdzeniem słuszności równania Schrödingera są także wyniki doświadczeń. Pojawia się jednak pytanie. ... A jak mierzyć wartości funkcji zespolonej? Pamiętamy jednak, że przy obliczaniu pochodnych (12.3.5) korzystaliśmy z z własności jednostki urojonej i, co miało wpływ na relacje pomiędzy pierwszą pochodną względem czasu i drugą względem współrzędnych, zawarte w równaniu Schrödingera. Gdyby równanie to nie zawierało jednostki urojonej, jego postać i rozwiązania byłyby zupełnie inne. Równanie to jest wiec równaniem dla funkcji zespolonej. Jaki jest jednak sens fizyczny takiej funkcji, która nie opisuje obiektów podlegających obserwacji doświadczalnej? Trzeba zmienić sposób myślenia, by przejść od opisu Newtona, do opisu Schrödingera.
Funkcja falowa nie opisuje bezpośrednio żadnych mierzalnych wielkości, choć
zawiera o nich informację. Informacja ta wyraża się poprzez kwadrat funkcji
falowej mający zawsze wartość rzeczywistą. Związek pomiędzy kwadratem
funkcji falowej a położeniem opisywanej przez nią cząstki wyrażony jest
przez gęstość prawdopodobieństwa określenia położenia cząstki. Gęstość
prawdopodobieństwa ![]() ,
podobnie jak gęstość materii określająca wartość masy w jednostce objętości,
wyraża prawdopodobieństwo tego, że położenie cząstki w chwili t
mieści się w odcinku o jednostkowej długości. Tak zdefiniowana gęstość
prawdopodobieństwa równa jest kwadratowi funkcji falowej
,
podobnie jak gęstość materii określająca wartość masy w jednostce objętości,
wyraża prawdopodobieństwo tego, że położenie cząstki w chwili t
mieści się w odcinku o jednostkowej długości. Tak zdefiniowana gęstość
prawdopodobieństwa równa jest kwadratowi funkcji falowej ![]() .
Właśnie ten związek nadaje sens fizyczny funkcji falowej.
.
Właśnie ten związek nadaje sens fizyczny funkcji falowej.
| (12.3.13) |
gdzie gwiazdka określa liczbę zespoloną sprzężoną, zgodnie z zasadami działania na liczbach zespolonych. Prawdopodobieństwo znalezienia cząstki na odcinku od x do x+dx określone jest więc jako iloczyn gęstości prawdopodobieństwa pomnożonej przez długość tego odcinka
| (12.3.14) |
W przypadku trójwymiarowym określamy prawdopodobieństwo znalezienia cząstki
w elemencie o objętości ![]() wokół punktu, którego położenie wyznacza promień wodzący
wokół punktu, którego położenie wyznacza promień wodzący ![]()
| (12.3.15) |
Prawdopodobieństwo znalezienia cząstki w całym rozważanym przez nas obszarze ma być równe jedności, co narzuca warunek w postaci
| (12.3.16) |
Jest to tzw. warunek normalizacyjny.
Sens fizyczny funkcji falowej poprzez prawdopodobieństwo określenia położenia cząstki w przestrzeni, różni się zasadniczo od sensu fizycznego wektora położenia cząstki w fizyce klasycznej. W tym ostatnim przypadku opisujemy ewolucję położenia ciała w sposób jednoznaczny za pomocą funkcji stanowiących rozwiązania równań Newtona, np. w ruchu harmonicznym lub w polu grawitacyjnym. Jeśli wyniki pomiarów różnią się od przewidywań teoretycznych, to albo wskutek niedokładności pomiarów albo przybliżeń opisu teoretycznego. W mechanice kwantowej mamy sytuacje zasadniczo różną.
W mechanice kwantowej nie określamy położenia cząstki, a określamy prawdopodobieństwo tego położenia. Wykonując więc pomiary położenia wielokrotnie w tych samych warunkach otrzymamy różne wyniki mające pewien rozkład statystyczny charakteryzujący "rozmycie" położenia w przestrzeni. Nie zawsze pomiar dotyczy położenia. Może dotyczyć innych wielkości, jak np. omawiana już niedokładność wyznaczenia pędu przy równoczesnym pomiarze pędu i położenia.
Związek funkcji falowej z określeniem mierzalnych wielkości fizycznych wiąże się z pojęciem tzw. paczki falowej. Paczka falowa stanowi sumę fal harmonicznych różniących się częstotliwościami, a więc i długościami fal (Porównaj to z nakładaniem się drgań równoległych w lekcji szóstej kursu Fizyka I.) Mówiąc o płaskiej fali harmonicznej o określonej długości widzimy obiekt nieskończony, tj. nieskończone powtarzanie się danej długości fali w określonym kierunku (nieskończony ciąg falowy). Jeżeli teraz nałożymy na siebie nieskończoną liczbę takich nieskończonych ciągów falowych różniących się długościami w pewnym nawet niewielkim przedziale wartości, to dzięki zachodzącej interferencji tylko w jednym obszarze wystąpią drgania w postaci paczki falowej dzięki interferencji konstruktywnej . Natomiast fale we wszystkich pozostałych obszarach zostaną dzięki interferencji destruktywnej wygaszone.
 |
W ten sposób z nieskończonych (niezlokalizowanych) obiektów (nieskończone ciągi falowe) otrzymujemy skończony obiekt zlokalizowany (paczkę falową), która reprezentuje cząstkę zlokalizowaną uwzględniając jej falowe własności. Uformowana w ten sposób paczka falowa może przemieszczać się w przestrzeni. Prędkość przemieszczania się paczki falowej, zwana prędkością grupową, odpowiada prędkości przemieszczania się cząstki. Paczka falowa stanowi również intuicyjny związek pomiędzy opisem obiektów klasycznych i kwantowych. Warto dodać, że właśnie forma paczki falowej stanowi element graficzny logo Wydziału Fizyki Politechniki Warszawskiej. |
| Rys. 12.3.1. Paczka falowa - logo Wydziału Fizyki PW |
Bardzo często mamy do czynienia z przypadkiem ruchu cząstek w polu określonym przez potencjał, który nie zmienia się w czasie. Energia potencjalna cząstki nie zależy wtedy od czasu i taki jej stan nazywamy stacjonarnym. Okazuje się, że w takich przypadkach można przedstawić funkcję stanowiącą rozwiązanie równania Schrödingera w postaci iloczynu dwóch funkcji, z których jedna zależy wyłącznie od położenia, a druga wyłącznie od czasu. Zapiszmy więc symbolicznie energię potencjalną cząstki i postać funkcji falowej dla takiego przypadku.
| (12.3.17) |
Kiedy taką formę funkcji falowej podstawimy do równania (12.3.9) i obliczymy pochodne, otrzymamy
| (12.3.18) |
Nie używamy już więcej symboli pochodnych cząstkowych, bowiem mamy do
czynienia z funkcjami tylko jednego argumentu. Dzieląc obustronnie przez ![]() otrzymujemy ciekawą formę równania, w której lewa strona zależy wyłącznie
od x, a prawa wyłącznie od t.
otrzymujemy ciekawą formę równania, w której lewa strona zależy wyłącznie
od x, a prawa wyłącznie od t.
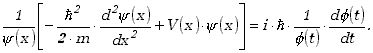 |
(12.3.19) |
Kiedy możliwe jest, by zachowana była równość obu stron równania, podczas gdy obie strony mogą się zmieniać niezależnie od siebie? (Pomyśl!)
Możliwe jest to tylko wtedy, kiedy ... zmieniać się nie mogą, czyli kiedy obie strony równania równe są tej samej stałej. Nazwijmy tą stałą - stałą separacji i oznaczmy, na razie, symbolem C. Otrzymujemy w ten sposób dwa niezależne równania.
| (12.3.20) |
 |
(12.3.21) |
Pierwsze z nich wyraża zależność funkcji falowej od czasu. Równanie to może być (po pomnożeniu obustronnym przez i ) przepisane w postaci
| (12.3.22) |
Kolejne pytanie - kiedy pochodna funkcji równa jest samej funkcji pomnożonej
przez stała, jak to ma miejsce w równaniu (12.3.22)? Relacja taka spełniona
jest dla funkcji ![]() .
Rozwiązaniem równania (12.3.22) jest więc funkcja
.
Rozwiązaniem równania (12.3.22) jest więc funkcja
| (12.3.23) |
Rozwiązanie to może też być przedstawione w postaci trygonometrycznej,
analogicznej jak we wzorze (12.3.2), gdzie ![]() ,
zaś
,
zaś ![]() jest częstotliwością fali. Ale, zgodnie z sugestią de Broglie'a częstotliwość
ta wiąże się z energią cząstki związkiem
jest częstotliwością fali. Ale, zgodnie z sugestią de Broglie'a częstotliwość
ta wiąże się z energią cząstki związkiem ![]() ,
wzór (12.1.1), skąd wniosek, że
,
wzór (12.1.1), skąd wniosek, że ![]() .
.
Uzyskaliśmy bardzo ważny rezultat. Stała separacji równa jest energii całkowitej
cząstki, dla której zależność czasowa opisywana jest funkcją ![]() .
Wynika stąd po pierwsze, że pełna funkcja falowa w polu stacjonarnym (niezależnym
od czasu) może być wyrażona w postaci
.
Wynika stąd po pierwsze, że pełna funkcja falowa w polu stacjonarnym (niezależnym
od czasu) może być wyrażona w postaci
| (12.3.24) |
a po drugie, że równanie Schrödingera niezależne od czasu (12.3.21) może być zapisane w formie
| (12.3.25) |
Zwróćmy uwagę, że w równaniu tym nie ma jednostki urojonej i
wiec funkcje falowe ![]() spełniające
to równanie nie muszą być funkcjami zespolonymi. Funkcje te nazywamy
funkcjami własnymi, zaś te wartości energii dla których istnieją rozwiązania
nazywamy wartościami własnymi.
spełniające
to równanie nie muszą być funkcjami zespolonymi. Funkcje te nazywamy
funkcjami własnymi, zaś te wartości energii dla których istnieją rozwiązania
nazywamy wartościami własnymi.