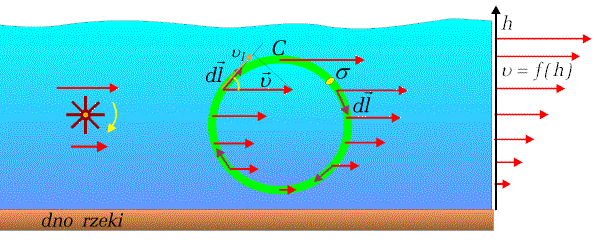
Zacznijmy od przykładu. W  rzece woda płynie powoli w pobliżu dna zaś szybciej przy swej powierzchni. Gdybyśmy w takim strumieniu umieścili wiatraczek podobny do tego, który pokazany jest na rysunku 1.5.1. to zacząłby się on obracać w kierunku wskazanym strzałką. Gdyby jednak prędkość wody była ta sama dla różnych wysokości albo wiatraczek ustawiony byłby w innej płaszczyźnie - pozostawałby nieruchomy. Przykład ten ilustruje nie omawiane przez nas dotychczas własności pola wektorowego, które charakteryzują wielkości zwane cyrkulacją i rotacją.

 Dla ich określenia wyróżnijmy w wodzie objętość w postaci wąskiej rurki o stałym przekroju . (Na rysunku 1.5.1 rurka ta pokazana jest kolorem zielonym.) W naszych dalszych rozważaniach będziemy zakładać, że mamy do czynienia z cieczą idealną, tj. nielepką i nieściśliwą. Oznaczmy przez wektor elementarnego przesunięcia się wody wzdłuż osi rurki w danym jej miejscu.  (Na rysunku wektory te pokazane są w kilku miejscach kolorem ciemnobrązowym.) Wektory prędkości wody w różnych punktach są różne i na ogół nie pokrywają się z kierunkami osi rurki. (Na rysunku pokazane są kolorem czerwonym.) Można jednak wyróżnić składową prędkości wzdłuż tej osi. (Składowa taka dla jednego wybranego punktu oznaczona jest na rysunku symbolem .) Wyrażenie (patrz rysunek) można przyjąć za miarę ruchu wody wzdłuż rurki w danym jej punkcie. W różnych punktach wartości tego wyrażenia będą różne, bo zarówno prędkość wody  jak i jej kierunek względem osi rurki mogą się zmieniać od punktu do punktu. (Kilka przykładów pokazanych jest na rysunku.) Obliczając jednak całkę z tego wyrażenia wzdłuż całej długości rurki stanowiącej zamknięty kontur, określamy wielkość zawierającą uśrednioną informację o cyrkulacji wody w rurce. Rzeczywiście, wyrażenia  mogą być większe i mniejsze, dodatnie i ujemne, ale ich suma obliczona dla całej rurki będzie uśrednioną miarą krążenia w niej wody co do ilości i co do kierunku. Całkę tę nazywamy cyrkulacją lub krążeniem wektora prędkości wzdłuż konturu i zapisujemy w postaci.

Ważną własnością cyrkulacji jest jej addytywność.  

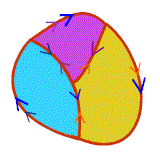Oznacza to, że gdybyśmy powierzchnię ograniczoną konturem podzielili na elementy i obliczyli sumę cyrkulacji po konturach tych elementów składowych, to otrzymalibyśmy wartość cyrkulacji po konturze . Wynika to natychmiast z faktu, że na odcinkach wspólnych tych składowych konturów znak cyrkulacji po jednym konturze będzie przeciwny do znaku cyrkulacji po drugim, zaś wartości będą równe. Spowoduje to ich redukcję czyli wzajemne znoszenie się. Nie będą redukować się jedynie cyrkulacje po zewnętrznych elementach konturu dając w rezultacie wartość cyrkulacji po całym konturze. Składowe kontury można dzielić dalej, co nie wpłynie na rezultat końcowy.

Rys.1.5.2. Ilustracja addytywnosci cyrkulacji