Rozważmy n-wymiarową próbę, czyli zmienną losową składającą się z n niezależnych elementów

.

(6.1.1)

 Wyznaczmy statystykę, tj. funkcje elementów tej próby zdefiniowaną jako średnia arytmetyczna

(6.1.2)

Tak zdefiniowana wielkość nosi nazwę wartości średniej  i jest także zmienną losową określoną przez wartości elementów próby i działanie arytmetyczne (suma), które je łączy. 

Wyznaczmy wartość oczekiwana tak zdefiniowanej wielkości

(6.1.3)

Widzimy, że:

1. Wartość oczekiwana dla wartości średniej z próby równa jest wartości oczekiwanej dla zmiennej losowej .
2. Równanie (6.1.3) jest słuszne dla każdego n, a więc jest to estymator nieobciążony.

Wyznaczmy teraz wariancję dla wartości średniej

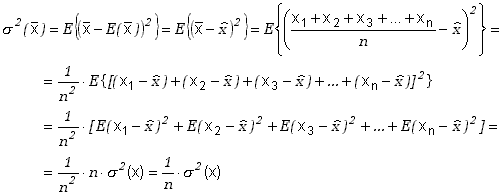(6.1.4)

Założyliśmy, że elementy próby są niezależne, a więc wszystkie kowariancje, czyli wartości oczekiwane dla znikają. W rezultacie otrzymaliśmy więc, że

(6.1.5)

Kiedy n zmierza do nieskończoności, to wariancja wartości średniej zmierza do zera. Wartość średnia jest więc estymatorem zgodnym wartości oczekiwanej . Zwróćmy uwagę, że skorzystaliśmy tu z założenia niezależności elementów próby . W praktyce, elementami tymi są często wielokrotne wyniki pomiarów danej wielkości. Pamiętajmy, że wyniki pomiarów powinny być wzajemnie niezależne, by wartość średnia prawidłowo odzwierciedlała wartość rzeczywistą mierzonej wielkości. 

Wartość średnia jest nieobciążonym i zgodnym estymatorem wartości oczekiwanej. Poszukajmy teraz estymatora wariancji. Narzucającą się definicją będzie wartość średnia sumy kwadratów różnic pomiędzy wartościami poszczególnych wyników pomiarów a wartością średnią czyli 

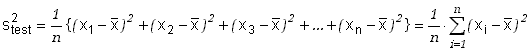(6.1.6)

Wyznaczmy wartość oczekiwaną tak określonej wielkości

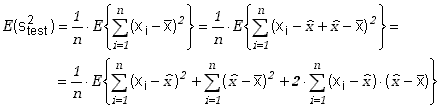(6.1.7a)

W zapisie takim zauważamy, że wyrażenia nie zawierające indeksów możemy wynieść przed znak sumy kontynuując dalej obliczenia

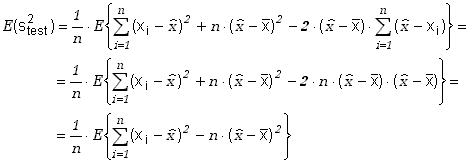(6.1.7b)

Pamiętając, że wartość oczekiwana sumy składników równa jest sumie ich wartości oczekiwanych kontynuujemy dalej obliczenia przenosząc znak wartości oczekiwanej pod znak sumy obejmującej teraz i drugi składnik w nawiasie klamrowym. Korzystamy też ze wzoru (6.1.4) pokazującego związek pomiędzy wariancją zmiennej losowej i wariancją wartości średniej 

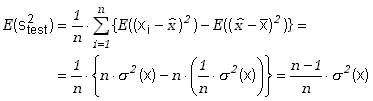(6.1.7c)

Wynik ten pokazuje, że jest estymatorem obciążonym, bo wartość oczekiwana zależna jest od liczby elementów próby i dla małej liczy n wartości oczekiwane tak zdefiniowanego estymatora są znacznie mniejsze niż wartość oczekiwana dla populacji. 

Defekt ten można łatwo usunąć przez wprowadzenie zmodyfikowanej definicji nieobciążonego estymatora wariancji w postaci

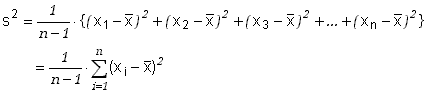(6.1.8)

W tak określonej definicji rozpoznajemy znany z laboratoriów fizycznych wzór na tzw. średnią kwadratową niepewność pojedynczego pomiaru. 

Rola czynnika 1/(n-1) staje się intuicyjnie jasna, kiedy weźmiemy pod uwagę, że zawsze możemy wyznaczyć wartość jednego z n pomiarów znając wartości n-1 pomiarów oraz wartość średnią. Liczba niezależnych elementów jest więc mniejsza o jeden w stosunku do liczby wykonanych pomiarów. Nie jest tak oczywiście, kiedy wariancję określamy względem znanej wartości rzeczywistej; wtedy właściwym czynnikiem jest 1/n. 

Zwróćmy na to uwagę wykonując obliczenia z pomocą kalkulatora posiadającego funkcje obliczeń statystycznych. Pozycja przycisku oznaczona zwykle symbolem s wyznacza wartość estymatora wariancji zgodnie ze wzorem (6.1.8) zaś pozycja oznaczona symbolem korzysta ze wzoru (6.1.6). Zrozumiałe jest, że różnice pomiędzy wynikami z użyciem różnych pozycji stają się niewielkie przy dużej liczbie sumowanych elementów. 

Wykorzystując związek (6.1.5) możemy zapisać wzór określający estymator wariancji wartości średniej 

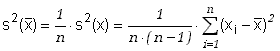(6.1.9)

Wzór ten znany jest również z zajęć w studenckich laboratoriach fizycznych. 

Zapiszmy jeszcze dla porządku wzory określające wprost wartości omawianych tu użytecznych estymatorów. 

Estymator odchylenia standardowego zwany średnią niepewnością kwadratową pojedynczego pomiaru 

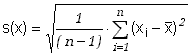(6.1.10)

Estymator odchylenia standardowego wartości średniej zwany średnią niepewnością kwadratową wartości średniej lub średnim kwadratowym błędem średniej.

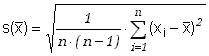(6.1.11)