Jeden z typowych problemów analizy danych ilustruje pokazany niżej rysunek

Funkcja korelacyjna dwóch mezonów "pi" (pionów). Symulacja komputerowa  wykonana przez studenta Wydziału Fizyki PW Zbigniewa Chajęckiego w ramach udziału grupy z W.F. PW w eksperymencie ALICE realizowanym w Europejskim Laboratorium Fizyki Cząstek CERN.

Różowym kolorem pokazana jest tzw. funkcja korelacyjna, której kształt opisuje czasowo-przestrzenny rozwój badanych reakcji jądrowych. Jest to symulacja komputerowa teoretycznego przebiegu tej funkcji. Układ pomiarowy ma jednak skończona zdolność rozdzielczą która wprowadza "rozmycie" funkcji teoretycznej i zmniejszenie jej wysokość. Również nie wszystkie rejestrowane cząstki są poprawnie identyfikowane, co też zmienia kształt funkcji korelacyjnej. Prawidłowo wykonana analiza danych powinna uwzględniać oba te efekty.

Rozmycie danego przebiegu funkcyjnego wskutek niepewności pomiarowych jest typowym przykładem splotu dwóch rozkładów, bardziej dokładnie - danego rozkładu z rozkładem normalnym. 

Jaki będzie rozkład zmiennej losowej stanowiącej sumę dwóch zmiennych losowych: i , tj. 

(5.4.1)

   Załóżmy, że zmienne i są wzajemnie niezależne, więc ich łączna gęstość prawdopodobieństwa może być wyrażona w postaci iloczynu

(5.4.2)

Dystrybuanta rozkładu zmiennej ma postać

(5.4.3)

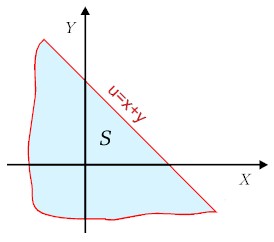Należy tu pamiętać o związku (5.4.1), co sprawia, że dla danej wartości u pojawiają się ograniczenia na zakresy zmiennych x i y. Ilustruje to rysunek 6.4.2. Rys. 6.4.2. Zakresy zmiennych losowych dla danej wartości ich sumy. Obszar S wyznacza zakres zmiennych przy obliczaniu dystrybuanty

Zgodnie z definicją dystrybuanty dla dwóch zmiennych mamy

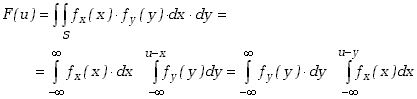(5.4.4)

Obliczając pochodną dystrybuanty możemy otrzymać funkcję gęstości prawdopodobieństwa dla zmiennej

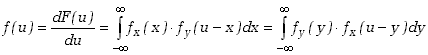(5.4.5)

Oczywiście, kiedy zmienne losowe i określone są w ograniczonym obszarze, to granice całkowania przyjmują skończone wartości.

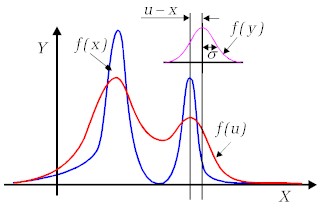
Powróćmy do pomiarów obarczonych niepewnościami przypadkowymi. Uzyskana w pomiarze wartość równa jest sumie wartości rzeczywistej i dystorsji pomiarowej, której wielkość określona jest przez konkretne  warunki eksperymentalne. Ilustruje to rysunek 5.4.3, gdzie kolorem niebieskim pokazana jest funkcja wyjściowa (niezniekształcona), a kolorem czerwonym funkcja będąca rezultatem pomiaru. Rys. 5.4.3. Splot rozkładu zmiennej losowej z rozkładem normalnym zmiennej losowej .

Gęstość prawdopodobieństwa zmiennej stanowiącej sumę ma w tym przypadku postać

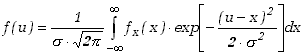(5.4.6)

W wyrażeniu podcałkowym mamy iloczyn danej funkcji i rozkładu normalnego. Granice całkowania określone są wiec faktycznie przez zakres zmienności tej funkcji.

Funkcja f(u) jest w przypadku pomiarów funkcją zmierzoną eksperymentalnie. Rozkład normalny określa niepewności pomiarowe w każdym zmierzonym punkcie. Wartość  f(u) w danym punkcie jest zgodnie ze wzorem (5.4.6) całką z iloczynu wartości funkcji niezniekształconych  (np. funkcji teoretycznej) pomnożonych przez funkcję gęstości rozkładu normalnego dla argumentu stanowiącego różnicę (u-x). Zauważamy natychmiast, że im mniejsza jest wartość odchylenia standardowego rozkładu normalnego w stosunku do różnicy (u-x) tym mniejszy zakres innych wartości funkcji f(x) będzie miał swój udział w wartości funkcji u. W konsekwencji mniej będzie zniekształcona funkcja wyjściowa.