| 3. Centralne twierdzenie graniczne i rozkład normalny (Gaussa) |
Tablica Galtona generuje rozkład kulek w przegródkach. Pokazaliśmy, że rozkład ten opisywany jest rozkładem dwumianowym. Gdybyśmy jednak wygenerowali kilka rozkładów spuszczając kilka razy po np. 200 kulek stwierdzilibyśmy, że wszystkie te rozkłady są różne. Nic dziwnego - to co wygenerowaliśmy, to nie są rozkłady prawdopodobieństwa ale rozkłady częstości rozproszeń kulki o daną liczbę przegródek względem środka tablicy.
Częstość ![]() występowania zdarzenia Aj, w n
próbach (np. rozproszenie kulki o j przegródek
w prawo) określamy następująco
występowania zdarzenia Aj, w n
próbach (np. rozproszenie kulki o j przegródek
w prawo) określamy następująco
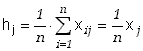 |
(5.3.1) |
W naszym przykładzie z tablicą Galtona n jest liczbą
spuszczonych kulek, a ![]() równe jest jeden gdy w i-tej próbie kulka rozprasza się o j
przegródek. Oczywiście, zdajemy sobie sprawę,
że częstość nie jest prawdopodobieństwem lecz także zmienną losową, bowiem jest różne w
różnych seriach doświadczeń (prób).
Wraz ze wzrostem liczby prób rozkład częstości
równe jest jeden gdy w i-tej próbie kulka rozprasza się o j
przegródek. Oczywiście, zdajemy sobie sprawę,
że częstość nie jest prawdopodobieństwem lecz także zmienną losową, bowiem jest różne w
różnych seriach doświadczeń (prób).
Wraz ze wzrostem liczby prób rozkład częstości
![]() będzie jednak swym kształtem zbliżał się do kształtu rozkładu dwumianowego.
Wartość oczekiwana częstości będzie więc zbliżać
się do wartości prawdopodobieństwa, bowiem mamy
będzie jednak swym kształtem zbliżał się do kształtu rozkładu dwumianowego.
Wartość oczekiwana częstości będzie więc zbliżać
się do wartości prawdopodobieństwa, bowiem mamy
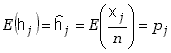 |
(5.3.2) |
zgodnie ze wzorem (5.1.12). Wzór (5.1.13) umożliwia wyznaczenie odchylenia standardowego
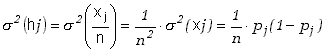 |
(5.3.3) |
Ciekawe jest spostrzeżenie, że iloczyn
![]() , który występuje
we wzorze (5.3.3) jest zawsze mniejszy od 1/4.
Wynika z tego natychmiast, że przy n wykonanych próbach
odchylenie standardowe częstości jest mniejsze od
, który występuje
we wzorze (5.3.3) jest zawsze mniejszy od 1/4.
Wynika z tego natychmiast, że przy n wykonanych próbach
odchylenie standardowe częstości jest mniejsze od
![]() . Wartość
ta określa więc niepewność statystyczną związana ze skończoną liczbą wykonanych prób.
Prawidłowość ta zwana jest prawem
wielkich liczb.
. Wartość
ta określa więc niepewność statystyczną związana ze skończoną liczbą wykonanych prób.
Prawidłowość ta zwana jest prawem
wielkich liczb.
Kiedy zwiększamy liczbę rzędów kółeczków na tablicy Galtona to zwiększamy liczbę elementarnych doświadczeń (odbicie kulki od kołeczka), których suma składa się na wynik jednego doświadczenia, jakim jest przejście kulki przez tablicę. Powstaje pytanie, jaki będzie kształt uzyskanego rozkładu, jeśli będziemy zwiększać do nieskończoności liczbę rzędów kołeczków. Oczywiście, będzie to w dalszym ciągu rozkład dwumianowy. Czy jednak można jego kształt przybliżyć jakimś innym rozkładem, podobnie jak przybliżyliśmy rozkład dwumianowy rozkładem Piossona przy spełnieniu określonych warunków.
Formułując to zagadnienie bardziej ogólnie zadamy pytanie jaki jest kształt rozkładu stanowiącego sumę zmiennych losowych pochodzących z rozkładu o zadanej wartości oczekiwanej i odchyleniu standardowym? Odpowiedź na to pytanie jest treścią jednego z fundamentalnych twierdzeń statystyki matematycznej tzw. centralnego twierdzenia granicznego. Twierdzenie to sformułujemy następująco
Jeżeli ![]() są niezależnymi zmiennymi losowymi pochodzącymi z rozkładów o wartościach
oczekiwanych równych
są niezależnymi zmiennymi losowymi pochodzącymi z rozkładów o wartościach
oczekiwanych równych ![]() i wariancjach równych
i wariancjach równych ![]() ,
to zmienna
,
to zmienna
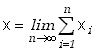 |
(5.3.4) |
ma rozkład normalny (Gaussa) o wartości oczekiwanej równej
![]() i wariancji równej
i wariancji równej ![]() .
.
Zapiszmy jeszcze raz to bardzo ważne twierdzenie.
Jeżeli
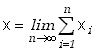 to
to
|
(5.3.4a) |
i przypomnijmy wzór określający rozkład normalny (Gaussa) w funkcji argumentu
x oraz parametrów:
![]() i
i ![]() .
.
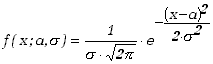 |
(5.3.5) |
Dowód tego twierdzenia można znaleźć w dowolnym podręczniku statystyki matematycznej. Przy formułowaniu założeń tego twierdzenia celowo zastosowana została liczba mnoga w odniesieniu do wartości oczekiwanych i wariancji sumowanych rozkładów, bowiem twierdzenie to jest słuszne także gdy sumowane zmienne losowe pochodzą z różnych rozkładów.
Centralne twierdzenie graniczne pokazuje, że rozkład Gaussa stanowi przypadek graniczny sumy wielkiej liczby niezależnych zmiennych losowych. Zauważmy, że odpowiada to właśnie omawianemu przez nas procesowi powstawania niepewności przypadkowych w pomiarach. To właśnie dzięki tej własności rozkład Gaussa jest jednym z najważniejszych rozkładów statystycznych w nauce i technice.
Porównajmy teraz trzy podstawowe rozkłady statystyczne: dwumianowy, Poissona i Gaussa i zobaczmy praktycznie warunki przejść granicznych pomiędzy tymi rozkładami.
| MS-Excel | Interaktywna ilustracja graficzna |
Kliknij w polu rysunku. |
| Rys.5.3.1 Rozkłady: dwumianowy, Poissona i Gaussa. | ||
Rozkład normalny dla n zmiennych losowych może być zapisany w postaci
|
|
(5.3.6) |
gdzie ![]() jest wektorem zmiennych niezależnych, których wartości oczekiwane dane są
wektorem
jest wektorem zmiennych niezależnych, których wartości oczekiwane dane są
wektorem ![]() ,
a macierz B jest odwrotnością macierzy kowariancji zmiennych
losowych
,
a macierz B jest odwrotnością macierzy kowariancji zmiennych
losowych ![]() tj.
tj.
|
|
(5.3.7) |
Współczynnik k określony przez warunek normalizacji dany jest wyrażeniem
|
|
(5.3.8) |
gdzie detB jest wyznacznikiem macierzy B.
W przypadku n=2 tj. dla dwuwymiarowego rozkładu normalnego, kiedy macierz kowariancji ma postać
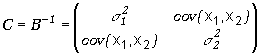 |
(5.3.9) |
macierz B, otrzymana przez odwrócenie macierzy kowariancji jest
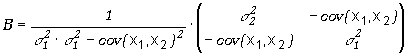
|
(5.3.10) |
Kiedy zmienne losowe ![]() i
i ![]() są niezależne, tzn. gdy znikają kowariancje pomiędzy tymi zmiennymi, macierz
B ma prostą postać
są niezależne, tzn. gdy znikają kowariancje pomiędzy tymi zmiennymi, macierz
B ma prostą postać
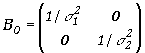 , ,
|
(5.3.11) |
zaś rozkład dwuwymiarowy ma postać iloczynu rozkładów jednowymiarowych
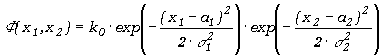 , ,
|
(5.3.12) |
gdzie stała normalizacyjna wynosi
|
|
(5.3.13) |
Kształt dwuwymiarowego rozkładu normalnego jest powierzchnią w przestrzeni trójwymiarowej, której rzuty na osie X1 i X2 , a także przekroje pionowe są rozkładami normalnymi. Przekroje poziome mają formę elipsy, zwanej elipsą kowariancji, której kształt zależny jest od odchyleń standardowych obu zmiennych i ich kowariancji. Punkty jeżące na tej samej elipsie odpowiadają temu samemu prawdopodobieństwu. Dla zerowych kowariancji i równych odchyleń standardowych elipsa przechodzi w okrąg, dla współczynnika korelacji równego jedynce, elipsa przechodzi w odcinek prostej.
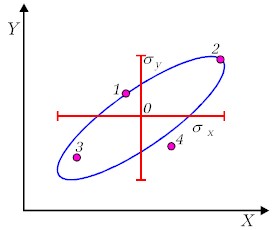 |
Rysunek obok pokazuje przykładowy kształt
elipsy kowariancji dla zmiennych skorelowanych. Zauważmy, że
prawdopodobieństwa odpowiadające punktom 1 i 2
są takie same, pomimo, że punkty te znajdują się w bardzo różnych
odległościach od punktu centralnego odpowiadającego największemu
prawdopodobieństwu, 0. Podobnie, prawdopodobieństwo
odpowiadające punktowi 3 jest większe niż to, odpowiadające
punktowi 4, chociaż punkt ten jest bardziej odległy od
punktu 0.
Wynika stąd bardzo ważny w praktyce analizy danych wniosek. W przypadku zmiennych skorelowanych nie wystarczy znać wartości odchyleń standardowych poszczególnych zmiennych, by zdawać sobie sprawę z niepewności danych wartości pomiarowych. Trzeba znać kształt elipsy kowariancji, która odzwierciedla relacje pomiędzy zmiennymi. |
| Rys. 5.3.1. Elipsa kowariancji |