Pamiętamy, że wartość oczekiwana w rozkładzie dwumianowym, wzór (5.1.7) jest iloczynem liczby prób i prawdopodobieństwa interesującego nas zdarzenia. Wynika z tego, że żądana wartość oczekiwana może być osiągnięta przez zmianę prawdopodobieństwa lub przez zmianę liczby prób. Rzeczywiście, gdyby pochylić tablicę tak, by prawdopodobieństwo rozproszenia w prawo, p, było o wiele mniejsze niż w lewo, to trzeba byłoby znacznie zwiększyć liczbę rzędów kołeczków, by kulka spadając odbijała się średnio tyle samo razy w prawo, co przy jednakowym prawdopodobieństwie odbicia w obie strony; gdy prawdopodobieństwo spóźniania się studentów na zajęcia jest bardzo małe, to dopiero przy bardzo licznych grupach przeszkadza to w prowadzeniu zajęć.

Kiedy w rozkładzie dwumianowym wzrasta wartość n dążąc do nieskończoności, a równocześnie maleje wartość p zdążając do zera, zaś ich iloczyn  (tj. wartość oczekiwana) pozostaje niezmieniony, to rozkład taki dąży do pewnego rozkładu, zwanego rozkładem Poissona. Rozkład Poissona ma ogromne znaczenie w analizie danych doświadczalnych (i nie tylko), dlatego warto poznać jego własności.

Zapiszmy rozkład dwumianowy w nieco innej postaci wykorzystując relację , gdzie pozostaje stałe.

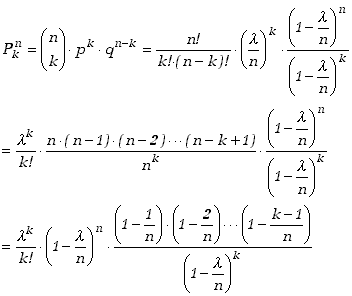(5.2.1)

Zauważmy, że kiedy n zdąża do nieskończoności, to wszystkie czynniki w ułamku z prawej strony ostatniej równości zmierzają do jedności, w rezultacie czego cały ułamek też dąży do wartości 1. Zachodzi także 

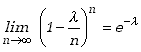(5.2.2)

co łatwo sprawdzić w tablicach matematycznych. Otrzymujemy więc, że 

(5.2.3)

Wyrażenie z prawej strony wzoru (5.2.3) określa wartość prawdopodobieństwa dla argumentu  k  z  rozkładu Poissona. Nietrudno sprawdzić wykorzystując postać rozłożenia w szereg funkcji , że rozkład ten jest rozkładem unormowanym do jedności tj.

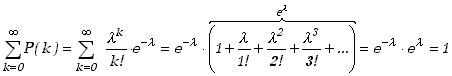(5.2.4)

Wartość oczekiwaną dla rozkładu Poissona wyznaczamy zgodnie z definicją 

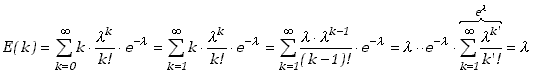(5.2.5)

Jest to niezwykle ważna własność rozkładu Poissona. Zapiszmy ją jeszcze raz dla zapamiętania

(5.2.6)

 W podobny sposób wyznaczmy odchylenie standardowe otrzymując

(5.2.7)

warto podać także wyrażenie na współczynnik asymetrii dla rozkładu Piossona. W tym celu wyznacza się najpierw współczynnik skośności tj. trzeci moment rozkładu względem wartości oczekiwanej

(5.2.8)

zaś współczynnik asymetrii rozkładu Poissona wynosi

(5.2.9)

Podsumujmy wiadomości o rozkładzie Poissona:

1. Rozkład Poissona stanowi graniczny przypadek rozkładu dwumianowego, gdy prawdopodobieństwo zdarzenia elementarnego zmierza do zera, a liczba prób zmierza do nieskończoności.
2. Rozkład Poissona zależny jest od jednego parametru, którym jest wartość oczekiwana,  .
3. Wariancja rozkładu Poissona równa jest wartości oczekiwanej, odchylenie standardowe równe jest wiec pierwiastkowi kwadratowemu z wartości oczekiwanej.
4. Współczynnik asymetrii dla rozkładu Poissona jest odwrotnością pierwiastka kwadratowego z wartości oczekiwanej. Oznacza to, że kiedy wzrasta wartość oczekiwana, to rozkład ten staje się coraz bardziej symetryczny.

 Kilka przykładów rozkładu Poissona zawiera rysunek poniżej. Uruchamiając ilustrację interaktywną można zobaczyć kształty oraz wartości prawdopodobieństw dla innych wartości parametru (lam*).