Ruch kulki na tablica Galtona to sekwencja zdarzeń, z których każde może mieć dwa warianty: rozproszenie w prawo, , i  rozproszenie w lewo, . Przestrzeń zdarzeń elementarnych składa się więc z dwóch elementów

(5.1.1)

Jeśli tablica jest idealnie symetryczna, to prawdopodobieństwa rozproszenia w lewo i w prawo są sobie równe i wynoszą 1/2. Jeśli nie jest symetryczna - są różne. Suma tych prawdopodobieństw zawsze jest jednak równa jedności czyli 

(5.1.1a)

Po pierwszym zdarzeniu natychmiast następuje drugie, po drugim trzecie itd. Każde rozproszenie jest więc oddzielnym doświadczeniem, którego wynik może przyjmować dwie wartości równe przesunięciu poziomemu kulki. Oznaczając wartość tego przesunięcia symbolem widzimy, że w pojedynczym rozproszeniu przesunięcie to jest równe . Liczba wszystkich rozproszeń (doświadczeń) równa jest liczbie rzędów kołeczków na tablicy. To, że kulka rozproszyła się w lewo (lub w prawo) nie znaczy bynajmniej, że następnym razem znów rozproszy się tak samo. Mówimy, że zdarzenia poszczególnych rozproszeń są od siebie niezależne.

Powstaje pytanie - o ile przesun ie się kulka po przejściu wszystkich rzędów kołeczków? Jeśli liczba ich rzędów wynosi n, i kulka rozproszyła się k razy w prawo i n-k razy w lewo, to rozproszenie końcowe będzie

(5.1.2)

Zapytamy teraz - jakie jest prawdopodobieństwo, że kulka przesunie się właśnie o tyle? Nazywając każde rozproszenie "próbą", zaś fakt rozproszenia w prawo "sukcesem", a rozproszenia w lewo "porażką", możemy to pytanie postawić bardziej ogólnie. Jakie jest prawdopodobieństwo k sukcesów w n wykonanych próbach (doświadczeniach).

Pamiętamy, że poszczególne zdarzenia są od siebie niezależne. Prawdopodobieństwo tego, że kuleczka rozproszy się k razy w prawo i n-k razy w lewo wynosi wiec .

Czy jest to już rozwiązanie problemu?  Wcale nie!  Zauważmy, że realizacja k rozproszeń w prawo i n-k w lewo może następować w różnej kolejności, tj. na wiele sposobów. Zależy to od samej wartości k. Jeśli k=n, to wszystkie rozproszenia muszą być w prawo i taka sytuacja realizuje się tylko na jeden sposób. Tak samo jest dla k=0. Intuicyjnie wyczuwamy, że największe liczby kombinacji będą dla k bliskiego n/2. 

Liczba możliwych kombinacji, w których dane zdarzenie realizuje się k razy w n próbach dane jest znanym z kombinatoryki wzorem 

(5.1.3)

 Prawdopodobieństwo tego, że kulka rozproszy się k razy (w dowolnej kolejności) w prawo przechodząc przez n rzędów kołeczków, czyli rozproszy się n-k razy w lewo, wynosi

(5.1.4)

W ten sposób zapisaliśmy wzór na rozkład dwumianowy wyrażający prawdopodobieństwo k sukcesów w n niezależnych próbach, kiedy każda próba może zakończyć się sukcesem lub porażką. 

Wyznaczmy wartość oczekiwaną i odchylenie standardowe dla rozkładu dwumianowego. Przypisując zdarzeniu będącemu sukcesem wartość 1, a będącemu porażką - wartość 0, mamy dla pojedynczej próby

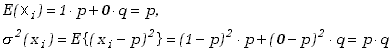(5.1.5)

Dla sumy n zdarzeń losowych, z których każde może przyjmować wartość zero lub jeden mamy, tj  dla

(5.1.6)

mamy

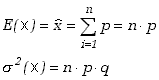(5.1.7)

gdzie skorzystaliśmy z założenia, że poszczególny próby są niezależne, tj. znikają wszystkie kowariancje.

Ruch kulki na tablicy Galtona, to tylko jeden z przykładów, gdzie realizowany jest proces prowadzący do rozkładu dwumianowego. Przykładów takich jest mnóstrwo wokół nas. Najczęściej podaje sie przykład n rzutów monetą rozważając liczbę przypadków, w których wypadnie np. reszka. Zauważmy jednak, że liczba studentów przychodzących punktualnie na zajęcia z KADD też podlega rozkładowi dwumianowemu, gdzie n jest liczbą studentów w grupie, a  p - prawdopodobieństwem punktualnego przyjścia studenta na zajęcia. 

Rozkład wielomianowy

Kiedy wynik pomiaru może przyjmować nie dwie ale więcej wartości to przestrzeń zdarzeń elementarnych składa się z wielu elementów

(5.1.8)

W danej próbie może wystąpić tylko jedno z tych zdarzeń. Są to więc zdarzenia wzajemnie wykluczające się. Podobnie jak w rozważanym poprzednio przykładzie rozproszenie może być albo w prawo albo w lewo lub w rzucie monetą: albo orzeł albo reszka a nigdy jedno i drugie razem, tak teraz przykładem może być rzut kostką do gry gdzie możliwości jest sześć, ale wynikiem próby jest tylko jedna z nich. Mamy więc

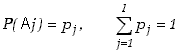(5.1.9)

Rozważania analogiczne do przeprowadzonych dla rozkładu dwumianowego prowadzą do wzoru na tzw. rozkład wielomianowy

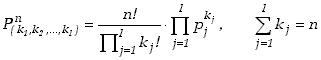(5.1.10)

Przypadkiem szczególnym tego rozkładu dla l=2 jest omawiany wcześniej rozkład dwumianowy. 

Określmy teraz zmienną losową tak, że jej wartość równa jest 1 gdy w wyniku i-tego pomiaru wystąpiło zdarzenie , zaś równa zeru, jeśli wystąpiło któreś z innych zdarzeń, np. określona wartość oczek w którymś z rzutów kostką do gry. Mamy wtedy

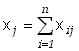(5.1.11)

zaś  wartość oczekiwana wyniesie

(5.1.12)

Elementy macierzy kowariancji równe są 

(5.1.13)

gdzie jest znanym z algebry symbolem (delta Kroneckera) równym jedynce, gdy i=j i zeru w przeciwnym przypadku. 

Na podkreślenie zasługuje fakt, że macierz kowariancji ma nieznikające elementy pozadiagonalne. Oznacza to występowanie korelacji pomiędzy zmiennymi. Pamiętamy, że zmiennymi są wartości przyporządkowane występowaniu jednego z wielu (ale nie nieskończenie wielu) zdarzeń, a prawdopodobieństwo ich występowania jest związane warunkiem (5.1.9). W związku z tym zauważamy natychmiast, że jeśli jedno zdarzenie występuje często, to pozostałe muszą występować rzadziej. Jest więc to korelacja negatywna.

Zobaczmy kilka przykładów rozkładu dwumianowego.Uruchamiając ilustrację interaktywną można zobaczyć kształty oraz wartości prawdopodobieństw dla innych wartości parametrów n oraz p.

Przykłady procesów prowadzących do rozkładu dwumianowego podane przez studentów

Przytoczone poniżej przykłady zostały wybrane z zadań domowych studentów według kryteriów: ciekawe, niezupełnie poprawne, śmieszne, aktualne, niekompletne,  itp.  Zastanów się nad każdym z nich. Czy wszystkie są poprawne? Czy wszystkie wymagane informacje w każdym z nich są podane? Jakich informacji i gdzie brakuje? Gdzie brakuje omówienia warunków procesu prowadzącego do rozkładu dwumianowego?  itd. Uwaga do wielu osób - przyjęte jest, że mówimy "liczba" - gdy chodzi o zbiór przeliczalny, np. liczba studentów w grupie, a mówimy "ilość" - gdy chodzi o zbiór nieprzeliczalny np. ilość wody w naczyniu.

1. Zakup gazety
n - ilość osób kupujących gazety np. tygodniki
p - prawdopodobieństwo że dana osoba kupi np. Newsweek'a
k - ilość osób, które kupiły np. Newsweeka

2. Studenci na WF,
n - ilość studentów studiujących na 2. roku na WF
p - prawdopodobieństwo zaliczenia 2. roku
k - ilość osób, które zaliczyły 2. rok

3. (przyklady pokojowe). Zakładamy ze pszczoły umieją sobie przekazywać informacje o znalezionych super kwiatkach ich pozycji. Pszczółka Maja znalazła takie coś i rozpowiada to n pszczółkom. Określamy:
p - prawdopodobieństowo tego ze pojedyncza pszczoła na podstawie opowiadania trafi do superkwiatkow.
n - liczba pszczół które o tym usłyszały.
Zmienną losową jest tu: możliwa liczba pszczół które dotarły do superkwiatkow.
(Założenie jest takie ze wszystkie po usłyszeniu o superkwiatkach chcą tam lecieć i wylatują od razu po usłyszeniu wiadomości, no i ze ich po drodze nie zaatakowały szerszenie bo się nie lubią z pszczołami).

4.
p- pawdop., że zjecie wyjdzie ostre,
q- prawdop.,że zdjęcie wyjdzie nieostre
n- liczba zdjęć na kliszy

5. Małe i duże ryby w stawie
n - liczba wszystkich ryb
k - liczba dużych ryb
p - prawdopodobieństwo złowienia dużej ryby

6. Wzrost ludzi pełnoletnich na Ziemi.
Przypuśćmy, że dzielimy wzrost na przedziały 1cm, od 150cm do 230cm. Prawdopodobieństwo spotkania określonej liczby osób o wzroście z danego przedziału będzie przykładem naszego rozkładu.
n - liczba przedziałów 1cm. n = 1,2,3...90,
k - konkretny przedział,
Najwięcej spotkamy osób o średnim wzroście. Małym o małym i dużym.

7. Urodziny  - może urodzić się chłopiec lub dziewczynka
n - liczba urodzin.
p - prawdopodobieństwo  urodzenia chłopca (1/2).
k - liczba urodzonych  chłopców   

8. Trafienie z ilością powyższych przykładów :
n - ilość studentów którzy oddali pracę.
p - prawdopodobieństwo tych którzy podali przynajmniej minimalną ilość przykładów.
q - prawdopodobieństwo tych którzy podali zbyt małą liczbę przykładów

=================