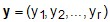 stanowi zestaw
liniowych funkcji zmiennych
stanowi zestaw
liniowych funkcji zmiennych 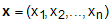 postaci:
postaci:|
|
Weźmy jako przykład funkcji zmiennych losowych przypadek liniowy, który ze względu na swą prostą strukturę znajduje częste zastosowania.
Wektor 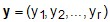 stanowi zestaw
liniowych funkcji zmiennych
stanowi zestaw
liniowych funkcji zmiennych 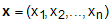 postaci:
postaci:
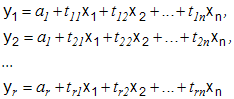 , , |
(4,3,1) |
co przyjmuje bardzo prostą postać w zapisie macierzowym
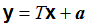 |
(4,3,2) |
gdzie T jest macierzą współczynników.
Wartość oczekiwana zmiennej y może być wyrażona w prosty sposób, pamiętając wzór (3,1,21) na wartość oczekiwana sumy zmiennych losowych
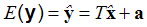 , , |
(4,3,3) |
Dla wyznaczenia macierzy kowariancji wykorzystamy wzór (4,1,16)
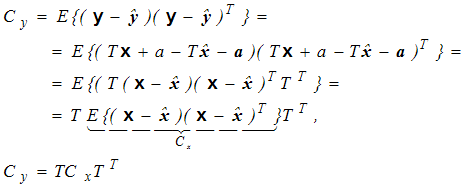 |
(4,3,4) |
Otrzymana zależność umożliwi wyznaczenie niepewności funkcji zmiennych losowych znane jako "prawo propagacji błedów". Jeśli znamy wartości oczekiwane oraz odchylenia standardowe i kowariancje zmiennych niezależnych (wartości mierzonych), to możemy obliczyć obliczyć niepewności funkcji tych zmiennych. Zakładamy, że niepewności wielkości mierzonych są względnie niewielkie, więc gęstość prawdopodobieństwa (wynik pomiaru) jest znacząca tylko w pobliżu wartości oczekiwanej (wartości rzeczywistej mierzonej wielkości). Mając to na uwadze możemy wykonać rozwinięcie w szereg Taylora:
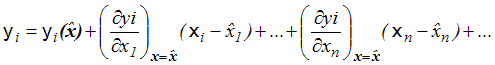 |
(4,3,5) |
gdzie zaniedbujemy wyrazy wyższego rzędu.
W zapisie macierzowym można to przedstawić nastepująco
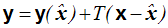 |
(4,3,6) |
zaniedbując znowu wyrazy wyższego rzędu. Macierz współczynników T ma w tym przypadku postać
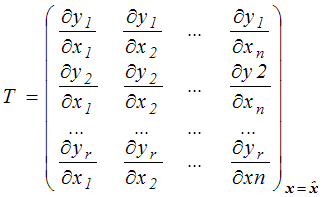 |
(4,3,7) |
Uzyskaliśmy w ten sposób postać macierzy współczynników T, która po wstawieniu do wzoru (4,3,4) umożliwia wyznaczenie macierzy kowariancji Cy. Elementy diagonalne tej macierzy, to poszukiwane wariancje zmiennych będących funkcjami wielkości pomiarowych. Zauważmy, że na ich wartości mają wpływ także pozadiagonalne elementy macierzy kowariancji Cx. Dopiero gdy znikają kowariancje pomiędzy zmiennymi niezależnymi (wielkości mierzone są niezależne) możemy stosować uproszczone wzory propagacji bledów.
Kiedy tak jest, wówczas elementy diagonalne macierzy kowariancji Cy wyrażają sie prostymi wzorami
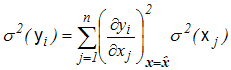 |
(4,3,8) |
W ten sposób uzyskujemy znany z pracowni fizycznej wzór
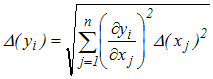 |
(4,3,9) |
Jest to właśnie wzór wyrażający "prawo propagacji błędów" (raczej - niepewności) . Pamiętajmy jednak, ze jest ono słuszne tylko w przypadkach gdy znikają niediagonalne elementy macierzy kowariancji, tj, gdy zmienne pomiarowe są nieskorelowane.