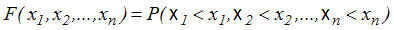Rozkłady te stanowią naturalne rozszerzenie wcześniej zdefiniowanych rozkładów dla jednej i dwóch zmiennych:

dystrybuanta rozkładu n zmiennych losowych:

,

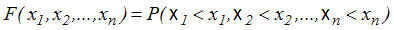(4,1,1)

gęstość prawdopodobieństwa:

,

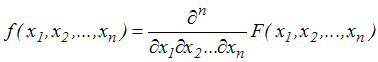(4,1,2)

gęstość prawdopodobieństwa rozkładu brzegowego zmiennej x_r  

,

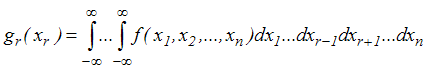(4,1,3)

wartość oczekiwana zmiennej x_r  

,

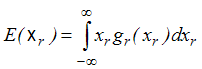(4,1,4)

wartość oczekiwana funkcji wielu zmiennych losowych

.

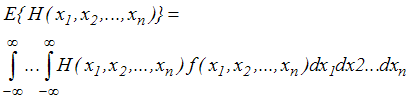(4,1,5)

Niezależność zmiennych losowych określa warunek 

.

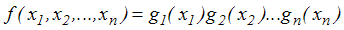(4,1,6)

Zwróćmy uwagę, że podobnie jak zdefiniowaliśmy brzegową gęstość prawdopodobieństwa dla zmiennej  x_r,  możemy określić łączną gęstość rozkładu brzegowego dla części zmiennych zachowując całkowanie po zmiennych pozostałych. Podobnie możemy określić warunek niezależności określonych  l spośród n zmiennych losowych.

Momenty 

Podobnie jak dla jednej i dwóch zmiennych, określamy momenty rzedu  l₁,l₂,...,l_n  dla wielu zmiennych, jako wartości oczekiwane funkcji 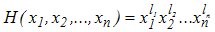. Mamy więc

.

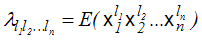(4,1,7)

Zwróćmy uwagę, że momenty pierwszego rzędu dla poszczególnych zmiennych, przy pozostałych -  rzędu zerowego, to po prostu wartości oczekiwane  

.

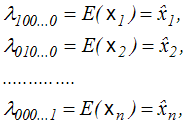(4,1,8)

Momenty centralne też definiujemy podobnie, jako momenty względem wartości oczekiwanych 

.

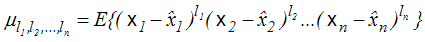(4,1,9)

Momenty centralne rzędu drugiego dla poszczególnych zmiennych, to wariancje:

.

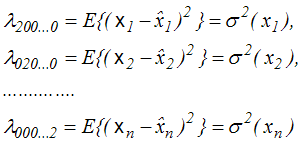(4,1,10)

Momenty centralne rzędu pierwszego dla zmiennych losowych x_i i x_j, czyli dla 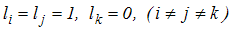 , to kowariancja pomiędzy tymi zmiennymi

.

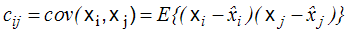(4,1,11)

Notacja wektorowa i macierzowa

W przypadku wielu zmiennych wygodnie jest stosować notacje wektorową i macierzową. Poszczególne zmienne losowe traktujemy wtedy jako składowe wektora 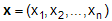w n wymiarowej przestrzeni. Zapiszmy dla przykładu wzory  (4,1,2) i (4,1,5) w nowej notacji

,

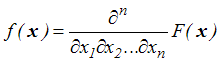(4,1,2a)

.

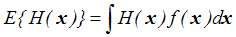(4,1,5a)

Dla zapisu wariancji i kowariancji wprowadzamy pojęcie tzw. macierzy kowariancji

.

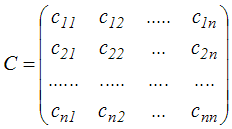(4,1,12)

Elementy macierzy kowariancji zdefiniowane są wzorem (4,1,12). Mamy zatem:

.

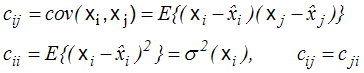(4,1,13)

Wartości oczekiwane w notacji wektorowej zapiszemy wzorem

.

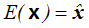(4,1,14)

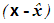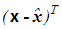Elementy macierzy kowariancji o wskaźnikach i oraz j można traktować jako wartości średnie tzw. iloczynu diadycznego wektorów oraz , gdzie pierwszy z wektorów jest wektorem kolumnowym, a drugi - wierszowym.

Iloczyn diadyczny, to iloczyn wektora kolumnowego przez wektor wierszowy. W rezultacie otrzymujemy

.

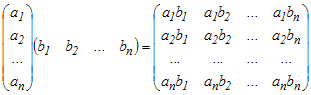(4,1,15)

Macierz kowariancji w notacji wektorowej zapiszemy więc wzorem

.

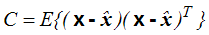(4,1,16)