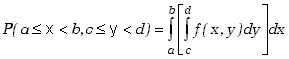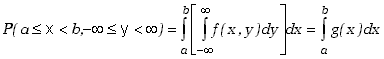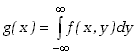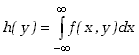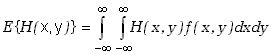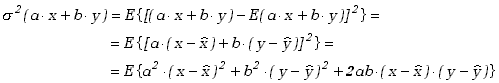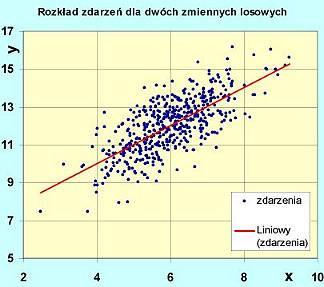
Zaczynamy tak samo, jak w przypadku jednej zmiennej. Potem zobaczymy, że rozkłady dwóch i wielu zmiennych losowych zawierają nowe elementy nie będące tylko uogólnieniem wiedzy o rozkładach jednowymiarowych.  <==( Przykład rozkładu zdarzeń dla dwóch zmiennych losowych obrazuje rysunek obok. Zdarzeniami mogą być np. wystąpienia opadów deszczu w funkcji położenia i w funkcji czasu. Zapiszmy wyrażenie określające dystrybuantę dla przypadku dwóch zmiennych losowych.
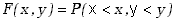
		(3.1.1)
	Jeśli F jest funkcją ciągłą zmiennych x i y, to możemy zdefiniować łączną gęstość prawdopodobieństwa zmiennych losowych  .

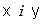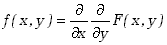(3.1.2)

Prawdopodobieństwo, że zdarzenie określone przez dane wartości zmiennych losowych znajdzie się w przedziale zmiennej x pomiędzy wartościami a i b, a w przedziale zmiennej y pomiędzy c i d  wynosi

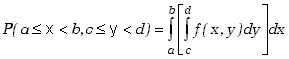(3.1.3)

Kiedy interesuje nas rozkład zdarzeń w funkcji jednej zmiennej tylko (np. prawdopodobieństwo opadów deszczu  dla różnych szerokości geograficznych) to należy przecałkować dwuwymiarowy rozkład gęstości prawdopodobieństwa po wszystkich wartościach drugiej zmiennej

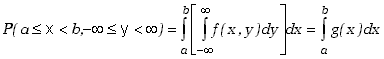(3.1.4)

gdzie

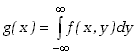(3.1.5

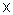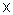jest gęstością prawdopodobieństwa zmiennej losowej . Taki rozkład nazywa się rozkładem brzegowym zmiennej . Oczywiście, analogicznie możemy określić rozkład brzegowy zmiennej . 

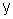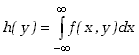(3.1.6)

Rozkład brzegowy jest więc rzutem rozkładu dwuwymiarowego na jedną z osi.

Podobnie jak  w rachunku prawdopodobieństwa określa się niezależność zdarzeń warunkiem by ich łączne prawdopodobieństwo było iloczynem prawdopodobieństw poszczególnych zdarzeń, tak i dwie zmienne losowe uważamy za niezależne jeżeli 

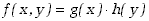(3.1.7)

Rysunek poniżej prezentuje przykład rozkładu dwuwymiarowego oraz jednego z rozkładów brzegowych. 

Funkcje dwóch zmiennych losowych

Podobnie, jak w przypadku jednej zmiennej losowej definiujemy wartość oczekiwaną funkcji H(x,y) dwóch zmiennych losowych

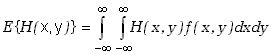(3.1.8)

  Analogicznie określamy też wariancję

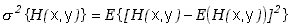(3.1.9)

Wartości oczekiwane i wariancje niektórych funkcji są szczególnie interesujące. Jeśli funkcja H zdefiniowana jest w postaci

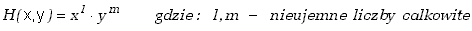(3.1.10)

to wartości oczekiwane, które oznaczymy symbolem 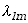, tak zdefiniowanej funkcji nazywamy momentami rzędu l i m względem . Mamy więc

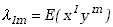(3.1.11)

Zauważamy natychmiast, że 

(3.1.12)

Kiedy więc funkcję H zdefiniujemy jako

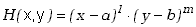(3.1.13)

to wartości oczekiwane tej funkcji 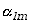, czyli

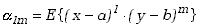(3.1.14)

stanowią momenty rzędu l i m względem punktów a i b. Kiedy zaś 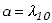, a 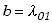, to otrzymujemy momenty względem wartości oczekiwanych poszczególnych zmiennych, :

.

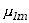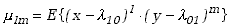(3.1.15)

Nietrudno zauważyć, że

.

(3.1.16)

oraz, że

.

(3.1.17)

Elementem nowym w naszych rozważaniach, nie mającym odpowiednika w przypadku rozkładów jednej zmiennej jest moment 

.

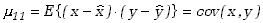(3.1.18)

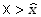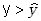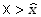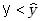Wielkość ta zwana jest kowariancją i charakteryzuje korelacje pomiędzy zmiennymi odgrywając bardzo ważna rolę w analizie danych. Zauważmy, że kowariancja ma wartość dodatnią wtedy, kiedy równocześnie oraz , zaś ma wartość ujemną gdy przy mamy . Oczywiście, kowariancja stanowi wartość uśrednioną i opisuje zbiór wszystkich rozpatrywanych zdarzeń. Kiedy wartości jednej zmiennej nie mają wpływu na wartości drugiej, czyli zmienne te nie są skorelowane, to kowariancja  równa jest zeru.

Wygodna w użyciu jest wielkość zwana współczynnikiem korelacji i zdefiniowana następująco

.

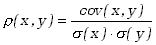(3.1.19)

Współczynnik korelacji charakteryzuje współzależność zmiennych 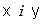przyjmując wartości z przedziału .

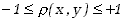Zapiszmy wartość oczekiwana i wariancję dla funkcji dwóch zmiennych losowych postaci

.

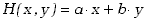(3.1.20)

gdzie a i b mają wartości  stałe. Wartość oczekiwana tej funkcji wynikająca z definicji (1.3.8) może być zapisana w postaci

.

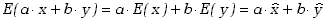(3.1.21)

Wariancję zapisujemy zgodnie ze wzorem (1.3.9)

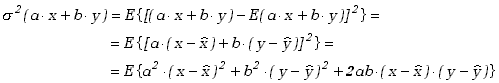(3.1.22)

czyli

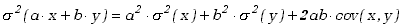(3.1.23)

Zauważmy, że wariancja sumy dwóch zmiennych losowych tylko wtedy równa jest sumie ich wariancji, pomnożonych przez kwadraty odpowiednich stałych, jeśli znika kowariancja, tj. jeśli zmienne te nie są skorelowane.