Moment bezwładności

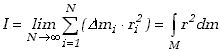
Ciało sztywne traktujemy jako układ nieskończenie wielu punktów materialnych, których wzajemne odległości pozostają niezmienione w czasie ruchu. Moment bezwładności dla ciała sztywnego wyznaczymy wiec zastępując sumowanie we wzorze (5.23) całkowaniem po całej objętości ciała. Odpowiada to wykonaniu przejścia granicznego

 gdzie jest elementem masy ciała znajdującym się w odległości od osi obrotu. Element masy możemy z kolei wyrazić przez element objętości, jeśli tylko znamy gęstość ciała w danym jego miejscu pamiętając, że . Wzór na moment bezwładności ciała sztywnego możemy więc zapisać w postaci

Kształt ciała można często przybliżać kształtem regularnych figur geometrycznych, co ułatwia wykonanie całkowania.  Gęstość materii może być jednak różna w różnych jego punktach. Jeśli ciało ma kształt prostopadłościanu, to celowe jest wykonanie całkowania w układzie współrzędnych prostokątnych. W układzie tym element objętości możemy zapisać jako i   wyrażenie na moment bezwładności względem osi pokrywającej się z osią Z ma postać

gdzie jest gęstością ciała w punkcie o współrzędnych .

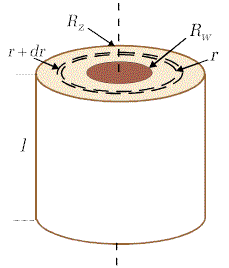Jako przykład obliczymy moment bezwładności wydrążonego walca o promieniu wewnętrznym  i zewnętrznym  względem osi pokrywającej się z osią symetrii i oznaczonej na rysunku linią przerwaną. W tym przypadku celowe jest wykonanie całkowania w układzie współrzędnych walcowych.  Zakładamy, że gęstość materii jest taka sama w całej objętości walca. Jako element objętości możemy przyjąć elementarny walec o promieniugrubości ścianki i wysokości . Jego objętość wynosi . Rys. 5.5 Wyznaczenie momentu bezwładności walca wydrążonego

Skorzystaliśmy tu ze wzoru na różnicę kwadratów, wzoru na objętość walca oraz faktu, że  iloczyn , to masa walca, którą oznaczyliśmy przez .

Rozpatrzmy dwa przypadki szczególne.

Kiedy promień wewnętrzny walca będzie równy zeru otrzymamy walec pełny. Otrzymujemy wzór na moment bezwładności pełnego walca względem osi przechodzącej przez środek walca wzdłuż jego wysokości:

Kiedy promień wewnętrzny stanie się bliski promieniowi zewnętrznemu mamy do czynienia z cienkościennym walcem, pierścieniem lub rurą. Otrzymujemy wtedy przybliżony wzór na moment bezwładności cienkościennego walca.

Zwróćmy uwagę, że jeśli masa w obu przypadkach jest taka sama, to moment bezwładności walca cienkiego jest dwukrotnie większy niż walca pełnego. Ma to wielorakie konsekwencje wykorzystywane w technice, o czym jeszcze powiemy w dalszej części tej lekcji. W podobny sposób można obliczyć momenty bezwładności dla innych kształtów ciał sztywnych.

Jeśli jednak oś obrotu usytuowana jest inaczej, wtedy i moment bezwładności będzie inny. W takich przypadkach całkowanie bywa bardziej skomplikowane. Można jednak pokazać, że jeśli znany jest moment bezwładności względem osi przechodzącej przez środek masy ciała, to moment bezwładności względem osi do niej równoległej i przesuniętej o odcinek dany jest wzorem

Wzór ten nosi nazwę twierdzenia Steinera.