 |
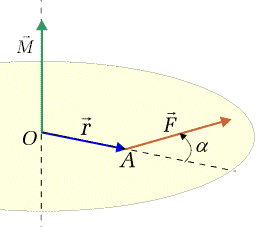
Na rysunku 5.3 pokazany jest schemat geometryczny ilustrujący
definicję momentu siły. Oczywiście, płaszczyzna, w której leżą
wektory Moment siły
|
Wielkością która dla ruchu obrotowego stanowi odpowiednik siły w ruchu postępowym jest moment siły. Moment siły zdefiniowany jest zawsze względem określonego punktu w przestrzeni, choć w czasie ruchu położenie tego punktu może się zmieniać.
|
Na rysunku 5.3 kolorem kremowym zaznaczona jest płaszczyzna wyznaczona przez
wektory ![]() i
i ![]() .
Zgodnie z definicją iloczynu wektorowego, wektor momentu siły jest prostopadły
do tej płaszczyzny. Zwrot tego wektora określony jest przez regułę śruby
prawoskrętnej. Bezwzględna wartość momentu siły wynosi
.
Zgodnie z definicją iloczynu wektorowego, wektor momentu siły jest prostopadły
do tej płaszczyzny. Zwrot tego wektora określony jest przez regułę śruby
prawoskrętnej. Bezwzględna wartość momentu siły wynosi
| (5.8) |
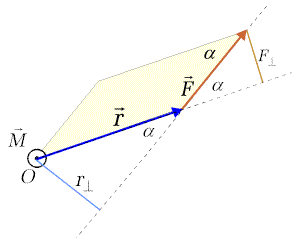 Rys.5.4. Rzut na płaszczyznę wyznaczoną przez wektor siły, |
Wartość momentu siły możemy wyrazić jako iloczyn siły przez składową promienia wodzącego prostopadłą do linii działania siły. Składową tą nazywamy ramieniem siły | |
|
|
(5.9) | |
| Możemy też wydzielić składową siły prostopadłą do promienia wodzącego. Wówczas wartość momentu siły możemy zapisać w postaci | ||
|
|
(5.10) | |
Widać, że wartość momentu siły określa składowa promienia wodzącego
prostopadła do kierunku działania siły lub składowa siły prostopadła do
promienia wodzącego. Kiedy kierunek siły pokrywa się z kierunkiem promienia
wodzącego moment siły równy jest zeru. Kolorem kremowym na Rysunku 3.3
zaznaczony jest równoległobok oparty na wektorach ![]() i
i ![]() .Pole tego równoległoboku
równe jest wartości bezwzględnej momentu siły. Kierunek wektora
momentu siły jest w tym przypadku skierowany prostopadle do ekranu, w naszą
stronę.
.Pole tego równoległoboku
równe jest wartości bezwzględnej momentu siły. Kierunek wektora
momentu siły jest w tym przypadku skierowany prostopadle do ekranu, w naszą
stronę.
Składowa siły prostopadła do promienia wodzącego nadaje przyspieszenie zgodne z kierunkiem ruchu punktu, znane nam z lekcji drugiej jako przyspieszenie styczne. Wykorzystując wzór (5.6b) Możemy więc napisać
|
|
(5.11) |
|
Wprowadzona tu wielkość
zwana momentem bezwładności, odgrywa zasadniczą rolę w opisie ruchu obrotowego i będzie omawiana szczegółowo w dalszej części tej lekcji Analogicznie określa się wektor momentu pędu. Jest on równy iloczynowi wektorowemu promienia wodzącego i pędu ciała.
|
Konstrukcje geometryczne nakreślone dla wektora momentu siły, możemy formalnie zastosować i dla wektora momentu pędu wstawiając wektor pędu w miejsce wektora siły, pamiętając oczywiście, że rozważamy różne wielkości fizyczne. Moment pędu jest równy zeru, jeśli kierunek pędu pokrywa się z kierunkiem promienia wodzącego. Zauważmy też, że kierunek momentu pędu pokrywa się z kierunkiem prędkości kątowej, jeśli promień wodzący jest prostopadły do osi obrotu. Możemy wtedy wyrazić w prosty sposób związek pomiędzy wartością momentu pędu i prędkością kątową.
|
|
(5.14) |
Skorzystaliśmy tu z faktu, że ![]() jest
prędkością ruchu obrotowego punktu i może być wyrażona przez iloczyn prędkości kątowej i promienia wodzącego, wzór (5.5). Następnie
wykorzystaliśmy wprowadzony wzorem (5.12) moment bezwładności.
jest
prędkością ruchu obrotowego punktu i może być wyrażona przez iloczyn prędkości kątowej i promienia wodzącego, wzór (5.5). Następnie
wykorzystaliśmy wprowadzony wzorem (5.12) moment bezwładności.
Zapiszmy teraz drugą zasadę dynamiki dla wektorów momentu siły i momentu
pędu. Pomnóżmy w tym celu obie strony równania (3.2) przez ![]() .
Otrzymujemy równanie
.
Otrzymujemy równanie
| (5.15) |
Widzimy, że lewa strona tego równania jest znanym nam już momentem siły. Dla znalezienia znaczenia fizycznego prawej strony obliczmy pochodną względem czasu momentu pędu.
| (5.16) |
Zauważamy natychmiast, że pierwszy człon po prawej stronie tego wzoru równy jest zeru. Wynika to z własności iloczynu wektorowego. Pochodna wektora promienia wodzącego względem czasu, to z definicji wektor prędkości, którego kierunek pokrywa się z kierunkiem pędu ciała, a iloczyn wektorowy dwóch wektorów równoległych jest równy zeru.
W rezultacie otrzymujemy.
| (5.17) |
Podstawiając ten związek do równania (5.15) i pamiętając w dalszym ciągu, że lewa strona równania (5.15) jest momentem siły (5.7), mamy
Wyraziliśmy w ten sposób druga zasadę dynamiki poprzez związek pomiędzy momentem siły i pochodna momentu pędu względem czasu. Związek ten jest zwany drugą zasadą dynamiki ruchu obrotowego. Zwróćmy uwagę, że równanie (5.18) będzie słuszne tylko w układzie inercjalnym, bowiem korzystaliśmy przy jego wyprowadzeniu z drugiej zasady dynamiki; nie będzie natomiast słuszny w układzie obracającym się. |