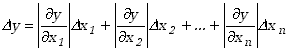
Kiedy przy kilkakrotnym wykonywaniu pomiaru uzyskuje się ten sam wynik,  mamy do czynienia z przewagą niepewności systematycznych nad przypadkowymi, kiedy wyniki są różne, większy jest udział niepewności przypadkowych.

 Weźmy jako przykład - pomiar napięcia w obwodzie elektrycznym.  Wykonując pomiar napięcia podręcznym woltomierzem wskazówkowym uzyskujemy na ogół wartość, która nie zmieni się jeśli powtórzymy pomiar. Gdybyśmy użyli precyzyjnego woltomierza cyfrowego okazałoby się, że ostatnia wskazana cyfra zmienia się, nawet  w czasie trwania pomiaru. W pierwszym przypadku, niepewności systematyczne woltomierza wskazówkowego były o wiele większe niż, występujące z pewnością również, niepewności przypadkowe. W drugim - woltomierz cyfrowy odnotowywał, nawet bardzo małe, przypadkowe zmiany napięcia. Rozpatrzymy przypadek pierwszy tj taki, w którym niepewności systematyczne są znacznie większe od niepewności przypadkowych. 

Przyjmujemy założenie, że niepewności zastosowanego przyrządu oraz odczytu wartości mierzonej przez wykonującego pomiar nie kompensują się, ale sumują. Określoną w ten sposób niepewność pomiaru nazywamy niepewnością maksymalną. 

Często mamy za zadanie wyznaczyć wielkość, która jest funkcją innych wielkości mierzonych, na przykład pole powierzchni walca na podstawie pomiaru jego średnicy i długości. Musimy wtedy uwzględnić zależność funkcyjną wielkości wyznaczanej od wielkości mierzonych. Najczęściej stosujemy metodę różniczki zupełnej. 

Metoda różniczki zupełnej 

Przyjmijmy, że chcemy ocenić niepewność wielkości  y, która jest funkcją mierzonych wielkości x₁, x₂, ... x_n, czyli y=f(x₁, x₂, ... x_n). Korzystając z rozwinięcia funkcji y w szereg Taylora wokół wartości będącej wynikiem pomiaru oraz  zaniedbując wyrazy wyższego rzędu niż pierwszy i zastępując nieskończenie małe przyrosty zmiennych niezależnych wartościami przyrostów skończonych otrzymamy

Zapis ten przypomina znane z matematyki pojęcie różniczki zupełnej, ale wartości bezwzględne pochodnych cząstkowych we wzorze (1.1.1) wynikają właśnie z naszego założenia o sumowaniu się przyczynków niepewności. Skończone przyrosty  wartości  x,  to niepewności  pomiarowe wielkości podlegających bezpośredniemu pomiarowi. Uzyskana w ten sposób wartość niepewności jest niepewnością maksymalną. Niepewność ta wyrażana jest w tych samych jednostkach w jakich wyrażona jest wartość zmierzona. Tak określona niepewność zwana jest  niepewnością bezwzgledną.

 Przykład:

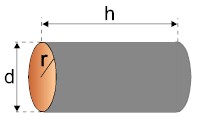W celu wyznaczenia objętości lub pola powierzchni walca mierzymy jego średnicę d oraz długość h. Mamy wtedy przyporządkowanie:  y - objętość lub pole powierzchni (których nie mierzymy bezpośrednio) oraz   x1 - średnica walca , d,   x2 - długość walca, h.

Kiedy rozważamy pomiar objętości walca mamy funkcję postaci 

W przypadku wyznaczania pola powierzchni walca mamy funkcję

Dla wyznaczenia niepewności pomiaru objętości obliczamy pochodne cząstkowe zgodnie ze wzorem (1.1.1); otrzymujemy

oraz

Zauważmy, że pochodna objętości walca względem średnicy zależy zarówno od samej średnicy, jak i od wysokości walca, zaś pochodna objętości względem wysokości od samej wysokości nie zależy, natomiast zależna jest od średnicy walca w kwadracie. Co z tego wynika?

Przyjmijmy na początek, że średnica walca wynosi d=20mm oraz, jego długość równa jest 10mm i że pomiary wykonano suwmiarką z dokładnością 0.1mm.  Otrzymujemy

Objętość walca równa jest zgodnie ze wzorem (1.1.2): . Niepewność względna objętości, tj. stosunek niepewności do wyznaczonej objętości walca wynosi . Zauważamy, że wkład do niepewności wyznaczenia objętości pochodzący od niepewności średnicy jest taki sam jak wkład pochodzący od niepewności długości. 

Przyjmijmy teraz, że średnica walca pozostaje bez zmian, d=20mm, a długość jest dziesięciokrotnie większa i wynosi h=100mm. W tym przypadku otrzymujemy  

W tym przypadku objętość walca równa jest  . Niepewność względna objętości wynosi teraz: . Widzimy, że tym razem wkład do niepewności objętości pochodzący od niepewności średnicy jest dziesięciokrotnie większy niż wkład pochodzący od niepewności długości. Ktoś może powiedzieć - "Jak to, przecież nie zmienialiśmy ani samej średnicy, ani niepewności jej pomiaru (!?)" Odpowiedź jest w postaci wzoru na pochodne cząstkowe i ich zależności od d i h. Wynika z tego, że w przypadku pomiaru długich prętów musimy znacznie bardziej dokładnie mierzyć ich średnice niż długości. Warto na przykład do pomiaru średnicy użyć śruby mikrometrycznej, podczas gdy do pomiaru długości wystarczy suwmiarka lub nawet tylko linijka milimetrowa. Podobne rozważania można przeprowadzić dla wyznaczenia pola powierzchni walca. 

Metoda różniczki logarytmicznej 

W przypadku, kiedy zależność funkcyjna ma postać iloczynowo/ilorazową możemy skorzystać z metody różniczki logarytmicznej. (Na przykład, z postacią taką mielibyśmy do czynienia przy wyznaczaniu objętości walca.)  Zapiszmy ogólnie taką funkcję dla dwóch zmiennych w postaci

(1.1.8)

gdzie a, n₁ oraz n₂ są wielkościami stałymi. Zlogarytmujmy obustronnie wyrażenie (1.1.8)

Zapisując teraz różniczkę logarytmu i traktując niepewności pomiarowe jako skończone przyrosty zmiennych niezależnych otrzymamy

Uzyskaliśmy w ten sposób nie wartość niepewności ale stosunek niepewności do samej wartości mierzonej. Stosunek ten, to niepewność względna, która jest wielkością bezwymiarową. 

Powróćmy do przykładu z wyznaczaniem objętości lub pola powierzchnia walca. Zauważamy natychmiast, że metodę pochodnej logarytmicznej możemy użyć wyłącznie do wyznaczenia objętości walca, która w swej zależności od d i h nie zawiera znaków dodawania ani odejmowania, ale nie możemy zastosować do wyznaczania pola powierzchni. Zapiszmy wzór na objętość walca w postaci analogicznej do wzoru (1.1.8)

Otrzymujemy stąd natychmiast wzór określający niepewność względną pomiaru objętości walca. Dla pierwszego z rozważanych przypadków tj. gdy średnica walca wynosi d=20mm oraz, jego długość równa jest 10mm

W drugim przypadku, tj. gdy d=20mm oraz h=100mm otrzymujemy

Dla uzyskania niepewności bezwzględnych  (wyrażonych w mm³) wystarczy pomnożyć niepewność względna przez wartość objętości. Metoda ta jest, jak widać, o wiele prostsza, choć mniej uniwersalna. Widzimy, że w tym przypadku klucz do znalezienia czynnika, który najmocniej wpływa na dokładność wyznaczenia danej wielkości w pomiarach pośrednich leży zarówno w dokładności pomiaru danej wielkości mierzonej jak i w wykładniku potęgi z jakim wielkość ta wchodzi do wzoru na wielkość wyznaczaną pośrednio.  

Przeprowadziliśmy tu rozważania na bardzo elementarnym poziomie. Ich celem nie była jednak nauka obliczania prostych pochodnych oraz elementarnej arytmetyki. Chodzi o to, by stosując dane wzory przy analizie wyników pomiarów, zdawać sobie sprawę z ich sensu fizycznego i pomiarowego, by nie stosować "na ślepo" wyuczonych wzorów, ale by rozumiejąc ich sens zaplanować odpowiednio metodę pomiarową, użyć odpowiednich instrumentów pomiarowych i wreszcie - właściwie zinterpretować sens fizyczny uzyskanego wyniku pomiaru.