W przestrzeni trójwymiarowej wektorem jest odcinek  posiadający określoną długość, kierunek i zwrot. Wektory przedstawiamy na rysunkach w postaci strzałki i oznaczamy zwykle małą literą z umieszczoną nad nią strzałką, np. , lub dwoma literami (na ogół dużymi), np. AB,  gdzie A oznacza początek, a B - koniec wektora. Prosta, na której leży wektor wyznacza jego kierunek, zaś strzałka określa jego zwrot, co ilustruje  Rys.1.

Rys.1. Wektor   i przeciwny mu wektor

Wektor nazywamy swobodnym, jeśli jego początek nie jest umiejscowiony w określonym punkcie przestrzeni. Wektor taki nie ulega zmianie jeśli jego początek zostanie przesunięty pod warunkiem, że jego długość, kierunek i zwrot nie  zmieniają się. W niektórych przypadkach położenie początku wektora jest istotne. Takie wektory nazywamy zaczepionymi, np. wektor, którego początek znajduje sie w punkcie A, jest wektorem zaczepionym w tym punkcie.

Wektor o długości jednostkowej nazywamy wersorem i oznaczamy na ogół małą literą z "daszkiem" np. . Jeżeli kierunek wektora zgodny jest  z kierunkiem danego wersora to możemy wektor ten zapisać w postaci , gdzie jest wielkością skalarną (liczbą) równą długości wektora ; Rys.2.. Długość (moduł) wektora oznaczamy też jako . Rys.2. Wersor  i wyrażony z jego pomocą wektor

Sumą dwóch wektorów jest wektor stanowiący przekątną równoległoboku skonstruowanego w ten sposób, że jeden z wektorów przesuwamy równolegle do jego kierunku tak, by początek tego wektora pokrył się z końcem drugiego. Sumę wielu wektorów (wypadkową) otrzymujemy dodając do sumy dwóch pierwszych wektorów następny wektor itd.  Różnica dwóch wektorów to suma wektora pierwszego i wektora przeciwnego do wektora drugiego tzn., Ilustruje to Rys. 3. Rys.3. Suma i różnica dwóch wektorów

Iloczyn danego wektora przez skalar , to inny wektor o tym samym kierunku, ale długości stanowiącej iloczyn długości wektora  przez wartość skalara i zwrocie zgodnym ze zwrotem wektora jeśli i przeciwnym gdy .

	Iloczyn skalarny dwóch wektorów  i jest liczbą (skalarem) określonym przez iloczyn
		(2)
Rys.4.  Wielkości określające iloczyn skalarny wektorów i	gdzie i , to długości wektorów, zaś jest kątem pomiędzy nimi, Rys.4.

Iloczyn wektorowy wektorów  i , to taki wektor , którego długość wynosi 

(3)

a kierunek jest prostopadły do kierunków obu wektorów i . Zależności te pokazane są na  Rys.5. Widać, że długość wektora równa jest polu równoległoboku wyznaczonemu przez wektory i .

Zwrot wektora jest taki, by układ wektorów , i był prawoskrętny. Układ jest prawoskrętny kiedy kierunek wektora zgodny jest z kierunkiem wkręcania śruby prawoskrętnej przy najkrótszym obrocie wektora do położenia wektora . Inaczej mówiąc - kiedy najkrótszy obrót wektora do położenia wektora odpowiada kierunkowi zginania palców prawej ręki, to kciuk wskazuje kierunek wektora . Należy pamiętać, że dla iloczynu wektorowego , tj. nie zachodzi prawo przemienności.

Rys.5. Wyznaczenie iloczynu wektorowego

Dobrym przykładem układu prawoskrętnego jest korkociąg. Obrotowi zgodnemu z ruchem wskazówek zegara towarzyszy ruch w kierunku do dołu (wkręcanie),  Obrotowi w kierunku przeciwnym towarzyszy ruch w górę (wykręcanie); porównaj ze schematem z lewej strony rysunku.

Rys.5a. Korkociąg - ilustracja układu prawoskrętnego.

Podwójny iloczyn wektorowy może być zapisany w postaci

,

(4)

 Uzyskany w ten sposób wektor leży w płaszczyźnie wyznaczonej przez wektory i .

 Wektory w układzie współrzędnych prostokątnych.

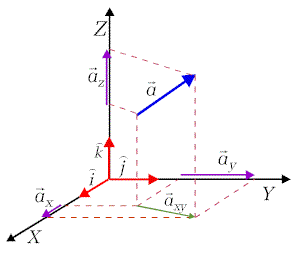Trójwymiarowy układ współrzędnych prostokątnych tworzą trzy osie wzajemnie prostopadłe przecinające się w jednym punkcie  stanowiącym początek układu współrzędnych. Na osiach obiera się jednostki miary, a kierunki osi określone są odpowiednio przez wersory , Rys. 5.  Tak określony układ jest układem prawoskrętnym tj. ruch obrotowy od osi w kierunku osi powoduje przesuwanie się śruby prawoskrętnej w kierunku osi . Rys.6. Wektor i jego składowe w układzie współrzędnych prostokątnych

Każdy wektor można przedstawić w układzie współrzędnych prostokątnych w postaci sumy trzech wektorów składowych. Na rysunku 6 pokazane są składowe wektora , które oznaczamy: . Wektor jest sumą

,

(5)

 Wielkości skalarne nazywamy współrzędnymi wektora . Wielkości te również określają wektor, co zapisujemy w postaci .

Długość wektora można wyznaczyć łatwo za pomocą jego współrzędnych, np. obliczając kwadrat wektora na podstawie wzoru ( 5) mamy 

,

(6)

(Przy podnoszeniu do kwadratu wzięliśmy pod uwagę, na podstawie wzoru (2), że kwadrat wektora to kwadrat jego długości, a iloczyny skalarne dwóch różnych składowych są równe zeru, bowiem kąt miedzy nimi jest kątem prostym, wiec jego cosinus równy jest zeru.) Długość wektora w układzie współrzędnych prostokątnych równa jest więc pierwiastkowi z sumy kwadratów jego współrzędnych.

 W układzie współrzędnych prostokątnych wyjątkowo łatwo wykonuje się operacje na wektorach. Współrzędne wektora będącego sumą  wyrażają się poprzez sumy współrzędnych wektorów i   

(7)

W podobny sposób zapisujemy współrzędne różnicy wektorów.

 Równie łatwo wyrazić jest wartość iloczynu skalarnego

(8)

Dla obliczenia iloczynu wektorowego należy zwrócić uwagę, że iloczyn wektorowy wersorów dwóch różnych osi układu prostokątnego równy jest wersorowi trzeciej osi ze znakiem dodatnim lub ujemnym zaś iloczyn wektorowy wersorów tej samej osi równy jest zeru. Mamy więc

(9)

(Dla otrzymania tego wyniku trzeba (pracowicie) wykonać serię mnożeń poszczególnych składników, zauważyć, że zamiana kolejności mnożenia dwóch wersorów odpowiada zmianie znaku  wersora trzeciego, a następnie uporządkować wyrazy otrzymanego wyrażenia.)