Funkcja pierwotna F(x) danej funkcji  y=f(x) - to taka funkcja, której pochodna równa jest  f(x) lub, co jest równoważne, której różniczka równa jest  f(x)dx.  

Wiemy, że pochodna stałej równa jest zeru. Wynika z tego, że dla dowolnej stałej C mamy

Jeśli więc funkcja jest funkcją pierwotną danej funkcji , to każda funkcja różniąca się od o stałą wartość jest także funkcją pierwotną funkcji . Funkcja ma więc nieskończenie wiele funkcji pierwotnych różniących się o wartość dowolnej stałej. 

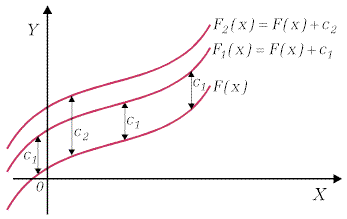Na rysunku obok krzywe F1(x) i F2(x) są identyczne z krzywą F(x)  i  otrzymane są przez równoległe przesuniecie krzywej F(x) wzdłuż osi Y o odcinki odpowiednio C1 i C2. Wszystkie trzy krzywe są funkcjami pierwotnymi danej funkcji f(x).

Zbiór wszystkich funkcji pierwotnych danej funkcji  f(x) nazywamy całką nieoznaczoną  funkcji  f(x), co zapisujemy w postaci. 

Mówimy, że całkę wyznaczamy z dokładnością do stałej dowolnej, którą nazywamy stałą całkowania

Kilka przykładów podstawowych całek (pominięto stałą całkowania)

Podstawowe reguły całkowania

1.	Stały czynnik ( c ) można wynieść przed znak całki
Wzór:
Przykład:
2.	Całka sumy (lub różnicy) funkcji równa jest sumie (lub różnicy) całek poszczególnych składników
Wzór:
Przykład:
3.	Całkowanie metodą podstawienia
Wzór:
Przykład:	( - stała);        podstawiamy:       różniczkując otrzymujemy: lub Mamy więc:
4.	Całkowanie przez części
Wzór:
Przykład:	przyjmujemy:     czyli   , otrzymujemy:

Całka oznaczona

Z definicji (1) wynika, że różnica funkcji pierwotnych wyznaczonych dla dwóch wartości a i b zmiennej x może być wyznaczona jako suma nieskończenie wielu różniczek . Suma taka,  to całka oznaczona funkcji w przedziale od granicy dolnej, a do granicy górnej b i może być zapisana jest w postaci

Wzór (4) wyraża  podstawowe twierdzenie rachunku całkowego, umożliwiające wyrażenie całki oznaczonej przez nieoznaczoną. Dla wyznaczenia całki oznaczonej w granicach od a do b należy znaleźć funkcję pierwotną  danej funkcji , wyznaczyć wartości tej funkcji w punktach x=a oraz x=b, a następnie obliczyć różnicę . W rezultacie odejmowania stała całkowania redukuje się, więc nie występuję przy obliczaniu całek oznaczonych. 

Rys 1. Geometryczna interpretacja całki oznaczonej.   Wyrażeniereprezentowane jest przez pole elementarnego paska o szerokości i wysokości , zaś całka oznaczona (4) równa jest polu figury pod krzywą i ograniczonej rzędnymi w punktach oraz . Przy zamianie granic całkowania w wyrażeniu (2) znak całki zmienia się na przeciwny.