KADD 2020 Laboratorium 12

From Łukasz Graczykowski

Zadanie

Dopasowanie funkcji za pomocą paietu MINUIT (5 pkt.)

Chcemy wykonać dopasowanie do danych doświadczalnych (wczytywanych z pliku) nie używając funkci Fit, tylko za pomocą pakietu MINUIT (dokumentacja), który daje nam zdecydowanie większą kontrolę nad procesem dopasowania funkcji.

Kroki postępowania

1. Ściągamy plik z danymi: example_data.root i wczytujemy go w funkcji głównej makra.

2. Do naszych danych dopasujemy taką oto funkcję zdefiniowaną jako funkcja globalna (nasz model opisujący dane doświadczalne):

double model(double x, double *par) 
{ 
 double mu    = par[3]; 
 double sigma = par[4]; 
 double norm  = 1./sqrt(2.*TMath::Pi())/sigma; 
 double G     = norm*exp(-0.5 *pow((x-mu)/sigma,2));  //unormowana funkcja Gaussa
 double BinWidth = hist->GetBinWidth(1); 
 return par[0] + par[1]*x + par[2] * BinWidth * G; 
}

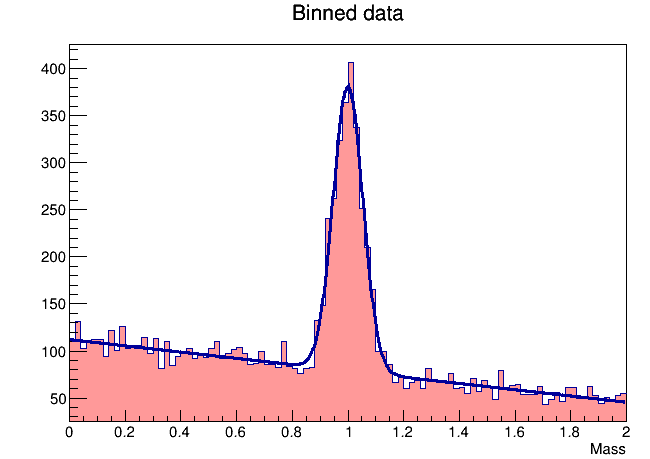
3. W funkcji głównej makra tworzymy obiekt TMinuit, przykładowo:

 TMinuit *gMinuit = new TMinuit(liczba_parametrow_fitu);

4. Musimy stworzyć funkcję globalną, którą MINUIT będzie starał się zminimalizować manipulując naszymi parametrami. Musi ona mieć postać typu:

void fcn(int &npar, double *gin, double &f, double *par, int iflag)

Uwaga 1! Nie przerażamy się parametrami (to są automatyczne parametry, które muszą być i które potrzebuje MINUIT, my ich w ogóle nie użyjemy).
Uwaga 2! Jedynym parametrem, który nas interesuje to double &f - to jest minimalizowana wielkość. W naszym przypadku chcemy, by f było po prostu tożsame z chi-kwadrat. To oznacza, że wewnątrz funkcji fcn musimy wykonać iterację bin po binie z wczytanego pliku i dla każdego binu policzyć kwadrat różnic ( (model-wartosc_binu)^2/niepwnosc_binu^2 ). Ostateczna wartość f, zgodnie z definicją chi-kwadrat, to po prostu suma kwadratów różnic dla wszystkich binów.

Wynik

Przykłądowy histogram z dopasowaniem:

Ostateczny output:

FCN=93.6468 FROM MINOS     STATUS=SUCCESSFUL    217 CALLS         364 TOTAL
                     EDM=3.79962e-17    STRATEGY= 1  ERROR MATRIX UNCERTAINTY   0.0 per cent
  EXT PARAMETER                  PARABOLIC         MINOS ERRORS        
  NO.   NAME      VALUE            ERROR      NEGATIVE      POSITIVE   
   1  p0           1.12163e+02   2.00576e+00  -2.00605e+00   2.00576e+00
   2  p1          -3.33062e+01   1.52150e+00  -1.52151e+00   1.52153e+00
   3  area         2.02070e+03   5.83151e+01  -5.82593e+01   5.83721e+01
   4  mean         1.00031e+00   1.70385e-03  -1.70425e-03   1.70425e-03
   5  width        5.34156e-02   1.50983e-03  -1.49782e-03   1.52309e-03
Info in <TCanvas::MakeDefCanvas>:  created default TCanvas with name c1