From Łukasz Graczykowski
Urząd statystyczny postanowił, w ramach okresowego badania populacji, zmierzyć wzrost pewnej reprezentatywnej grupy studentów. Do opracowania wyników badania niezbędne jest: policzenie średniego wzrostu studentów z badanej próbki, odchylenia standardowego wartości średniej, oraz posortowanie danych.
Plik z danymi ma następujący format:
liczba_studentów
wzrost1
wzrost2
…
Do wykonania:
- Stworzyć (dynamicznie!) tablicę liczb rzeczywistych (
float lub double) o rozmiarze danym liczbą zbadanych studentów i wczytać do niej z zewnętrznego pliku dane.
- Wypisać na ekran tablicę danych – funkcja zewnętrzna:
void wypisz(const float* tab, int n) (1 p.)
- Obliczyć i wypisać na ekran wartość średnią wczytanej próbki danych – funkcja zewnętrzna:
float srednia(const float* tab, int n) (1 p.)
- Obliczyć i wypisać na ekran odchylenie standardowe wartości średniej (jak policzyć odchylenie standardowe – patrz Uwaga 1 poniżej) – funkcja zewnętrzna:
float odchStd(const float* tab, int n) (1 p.)
- Zaimplementować funkcję sortującą dane za pomocą algorytmu sortowania przez wstawianie, tzw. Insert Sort (patrz Uwaga 2 poniżej) – funkcja zewnętrzna:
void sortuj(float* tab, int n) (2 p.)
Dodatkowo: jeśli ktoś skończy wcześniej, program powinien działać w pętli while, a każda z powyższych opcji powinna być realizowana za pomocą odpowiedniej opcji używając switch-case. Wprowadzamy również zewnętrzną funkcję void menu(), która w pętli wyświetla za każdym razem informację z menu użytkownika. (+0.5 p.)
Plik z danymi: wzrost.txt
Uwaga 1! Odchylenie standardowe wartości średniej:
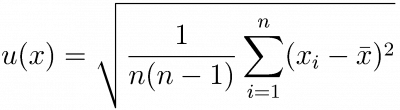Aby policzyć pierwiastek z liczby używamy funkcji sqrt (dla typu double; lub jej wariantu sqrtf dla typu <code?float</code>):
double sqrt (double x);
float sqrtf (float x);
Należy dołączyć bibliotekę: math.h
Uwaga 2! Tym razem do sortowania tablicy wykorzystamy algorytm tzw. "sortowania przez wstawianie" (insertion sort):
Lista kroków (przykład dla n-elementowej tablicy):
K01: Dla j = n - 2, n - 3, ..., 0: wykonuj K02...K04
K02: x ← tablica[j]; i ← j + 1
K03: Dopóki ( i <= n ) ∧ ( x > tablica[i] ): wykonuj tablica[i - 1] ← tablica[i]; i ← i + 1
K04: tablica[i - 1] ← x
K05: Zakończ
PS. Algorytm sortowania przez wstawianie ma podobną złożoność obliczeniową (O(n^2)) jak poznany już algorytm sortowania bąbelkowego. W sortowaniu bąbelkowym zawsze porównujemy wybrany element z największym (najmniejszym) i wstawiamy w odpowiednie miejsce w tablicy. W sortowaniu przez wstawianie mamy dodatkowo dwa regiony (posortowany i nieposortowany), wybrany element wstawiamy na odpowiednie miejsce w posortowanym regionie. Zatem algorytm ten będzie działał szybciej, jeżeli tablica wejściowa jest w dużej części już posortowana. Trochę jak z kartami: najpierw mamy dwie karty, układamy je w założonej kolejności, potem dokładamy trzecią i wkładamy w odpowiednie miejsce, dobieramy czwartą i znowu wkładamy w odpowiednie miejsce, itd. W sortowaniu bąbelkowym przestawiamy kolejne elementy obok siebie.
