KADD 2022 Laboratorium 2 EN

From Łukasz Graczykowski

Revision as of 12:13, 7 March 2022 (view source) Lgraczyk (Talk | contribs) (Created page with "{| align="right" | __TOC__ |} ==Zadanie== Let X be a random variable that has a probability distribution function f(x): File:wzor_lab2.png Please do: * Draw the probabilit...") ← Older edit		Latest revision as of 12:14, 7 March 2022 (view source) Lgraczyk (Talk | contribs) (→Results)
Line 25:		Line 25:
	Output:		Output:
-	P(5<X<10) z gestosci: 0.245723	+	P(5<X<10) from the density: 0.245723
-	P(5<X<10) z dystrybuanty: 0.245723	+	P(5<X<10) from the cumulative distribution: 0.245723
-	Srednia z funkcji TF1: 5.98798	+	Mean from the function TF1: 5.98798
-	Srednia analitycznie: 6	+	Mean analytically: 6
-	Wariancja z funkcji TF1: 35.3988	+	Variance from TF1: 35.3988
-	Wariancja analitycznie: 36	+	Variance analytically: 36
-	Moda: 0	+	Mode: 0
	x0.25: 1.74		x0.25: 1.74
	x0.5: 4.16		x0.5: 4.16
	x0.75: 8.32		x0.75: 8.32

---

Latest revision as of 12:14, 7 March 2022

Contents 1 Zadanie 2 Results

Zadanie

Let X be a random variable that has a probability distribution function f(x):

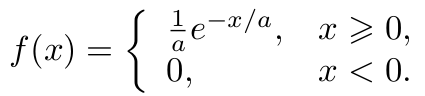
Please do:

• Draw the probability distribution function f(x) (0.5 pkt)
• Draw the cumulative distribution F(x). Cumulative distribution has to be drawn numerically and analytically. (1 pkt)
• Calculate the probability P(5 <= X <= 10) (0.5 pkt)
• Calculate the expected value E(X) and compare with the analytic result (1 pkt)
• Calculate the variance V(X) and compare with the analytic result(1 pkt)
• Calculate mode (0.5 pkt)
• Calculate quantiles: (0.5 pkt)
  • lower quartile
  • median
  • upper quartile

Results

Plots:

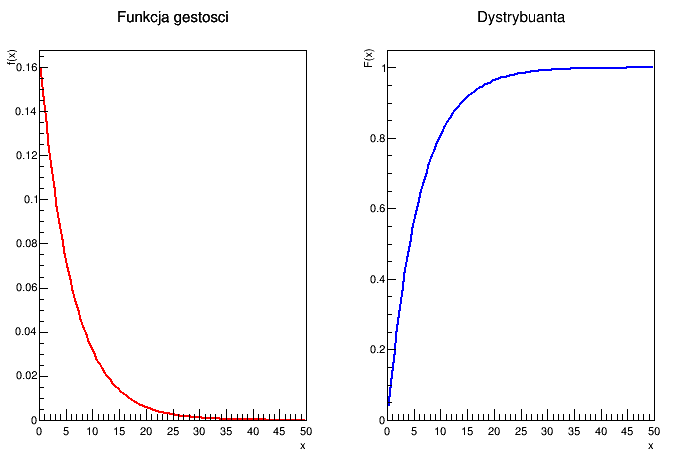
Output:

 P(5<X<10) from the density: 0.245723
 P(5<X<10) from the cumulative distribution: 0.245723
 Mean from the function TF1: 5.98798

 Mean analytically: 6
 Variance from TF1: 35.3988
 Variance analytically: 36
 Mode: 0
 x0.25: 1.74
 x0.5: 4.16
 x0.75: 8.32