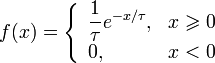KADD 2017 Zadanie 6

From Łukasz Graczykowski

---

Revision as of 06:31, 27 March 2017

Contents 1 Zadanie 2 Uwagi 3 Wynik

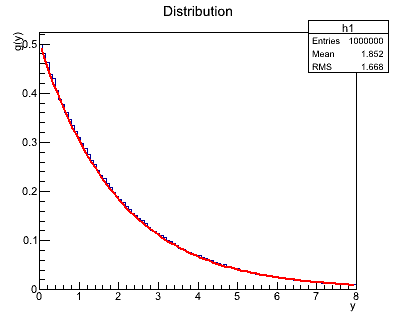
Zadanie

Część pierwsza: liniowy kongruentny generator liczb losowych (1 pkt.)

Należy napisać generator liczb pseudolosowych oraz zapisać wygenerowane liczby do pliku.

Stworzony generator powinien opierać się na wzorze:

x[j+1] = (g*x[j] + c) mod m.

Generator taki nazywamy generatorem LCG - czyli generatorem liniowym kongruentnym. Zadanie pewnej wartości poczatkowej x[0] definiuje nam zatem cały ciąg, który ponadto jest ciągiem okresowym. Okres zależy od doboru parametrów i przy spelnieniu kilku warunków osiąga maksymalnie wartość m. Warunki te to:

• c i m nie maja wspolnych dzielników,
• b = g-1 jest wielokrotnoscia kazdej liczby pierwszej p, ktora jest dzielnikiem liczby m,
• b jest wielokrotnością 4 jesli n tez jest wielokrotnością 4.

Dla uproszczenia należy przyjąć c = 0, otrzymując w ten sposób multiplikatywny liniowy generator kongruentny (MLCG).

• Wartości g oraz m powinny być łatwe do modyfikacji w programie.

Efektem działania makra powinien być plik nazwa.dat zawierający ciąg wygenerowanych liczb dla zadanych parametrów. Makro należy uruchomić trzy razy, otrzymując trzy pliki: losowe1.dat, losowe2.dat, losowe3.dat, dla parametrów odpowiednio:

• m=97 i g=23,
• m=32363 i g=157,
• m=147483647 i g=16807.

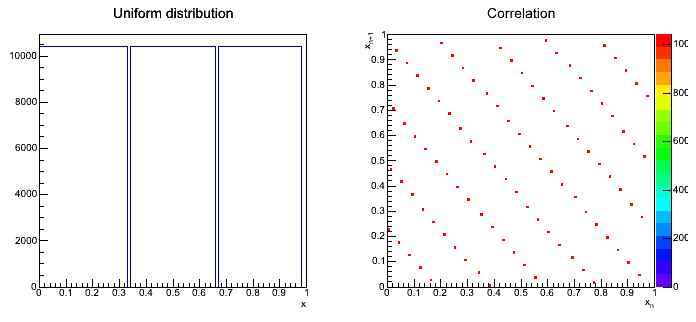
Część druga: test widmowy (1 pkt.)

Należy przeprowadzić test widmowy aby przetestować jakość generatora. By to zrobić należy narysować na płaszczyźnie punkty o współrzędnych (x[n], x[n+1]). Uzyskany obraz utworzy wzór przypominający widmo generatora - stąd nazwa testu.

Jeśli punkty będą rozłożone równomiernie generator można uznać za dobry. Jeśli zdecydowanie widać pewną okresowość - punkty powtarzają się wielokrotnie - generator nie działa poprawnie. Oczywiście na rozłożenie punktów wpływa jedynie dobór parametrów g i m.

• Do tworzenia wykresów widma poleca się użycie obiektów TH2D.

Wynikiem powinny być trzy wykresy widma.

Część trzecia: generacja liczb losowych oparta na transformacji rozkładu jednorodnego (3 pkt.)

Dowolna funkcja zmiennej losowej jest zmienną losową. Powstaje więc pytanie jaka jest gęstość zmiennej losowej Y jeżeli znana jest gęstość f(x). Zakładamy, że prawdopodobieństwo g(y)dy jest równe f(x)dx, gdzie dx odpowiada wartością dy. Warunek jest spełniony dla odpowiednio małych dx. Wynika stąd, że:

g(y) = dx/dy f(x)

Teraz jeżeli założymy, że gęstość prawdopodobieństwa f(x) wynosi 1 w 0<=x<=1 i f(x) = 0 dla x<= 0 i x>1 to powyższe równanie możemy zapisać w postaci:

g(y)dy = dx = dG(y),

gdzie G(y) jest dystrybuantą zmiennej losowej Y. Co po całkowaniu daje nam

x = G(y) => y = G^-1(x).

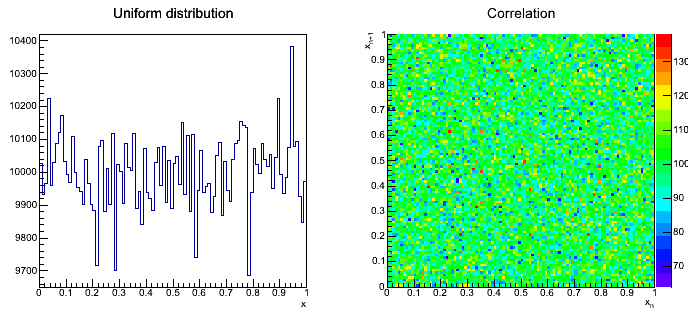
Jeśli zmienna losowa X ma rozkład jednostajny na odcinku pomiędzy 0 i 1 oraz jeśli znana jest funkcja odwrotna G^-1(x) to funkcja g(y) opisuje gęstość prawdopodobieństwa rozkładu zmiennej losowej Y.

Używając tej metody należy wygenerować 10000 liczb z rozkładu:

Dla tau = 2:

• Należy wygenerować 10000 liczb z rozkładu 0 do 1 używając generatora z części pierwszej.
• Analitycznie (na kartce) policzyć dystrybuantę tego rozkładu, a następnie funkcję odwrotną. (1 pkt.)
• Wygenerować rozkład f(x) - wrzucając wygenerowane wartości do histogramu - korzystając z: (1 pkt.)
  • liczb wygenerowanych wcześniej i wczytanych z plików losowe1.dat, losowe2.dat, losowe3.dat,
  • standardowego generatora ROOT'a gRandom->Rndm(1).
• Narysować na jednym wykresie histogram (odpowiednio unormowany) oraz funkcję teoretyczną f(x) (obiekt TF1). (1 pkt.)

Uwagi

• Wczytywanie danych z pliku:

ifstream ifile;
ifile.open("dane.dat");
double val;
while(ifile>>val)
{
  cout<<val<<endl;
}
ifile.close();

• Zapisywanie danych do pliku:

ofstream ofile;
ofile.open("dane.dat");
for(int i=0;i<N;i++)
  ofile<<val<<endl;
}
ofile.close();

Wynik

Przykładowy rozkład dla parametrów:

• m=97, g=23

• m=2147483647, g=16807

Przykładowy wynik transformacji rozkładu jednorodnego: