From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 19: |
Line 19: |
| | * Wszystkie wielkości (stałą c, dystrybuantę, gęstości brzegowe) wyznaczamy numerycznie np. wykorzystując metodę <code>Integral</code>. | | * Wszystkie wielkości (stałą c, dystrybuantę, gęstości brzegowe) wyznaczamy numerycznie np. wykorzystując metodę <code>Integral</code>. |
| | * Skrytp powienien być napisany w taki sposób aby wykonywał obliczenia dla dowolnego m i n. | | * Skrytp powienien być napisany w taki sposób aby wykonywał obliczenia dla dowolnego m i n. |
| - | * Skrypt nie działąjący, tzn. zawierający błędy składni nie będzie podlegał ocenie. | + | * Należy oznaczyć i podpisać wszystkie osie. |
| - | * Za elementy, które są obliczane niepoprawnie przyznawane będzie 0 pkt. Proszę się upewnić, że rysowane krzywe lub powierzchnie są prawidłowe. | + | * Funkcje rozkladu gestosci (obiekt TF2) tworzymy poprzez wykorzystanie funkcji jak |
| | + | poniżej (odpowiednio zdefiniowanej dla wszystkich wartości x i y) |
| | | | |
| | == Wynik == | | == Wynik == |
Revision as of 09:12, 5 March 2012
Zadanie
Dana jest gęstość prawdopodobieństwa:
Failed to parse (Missing texvc executable; please see math/README to configure.): f(x,y)=\left\lbrace \begin{array}{ll} cx^{m}y^{n},&0\leqslant x\leqslant 1 \,\wedge\, 0\leqslant y\leqslant 1\\0,&\text{pozostale przypadki}\end{array}\right.
Należy dla parametrów m=1 i n=2:
- wyznaczyć stałą c w taki sposób aby rozkład gęstości był unormowany (1pkt)
- narysować gęstość prawdopodobieństwa f(x,y) (1pkt)
- wyznaczyć i narysować dystrybuante F(x,y) (1pkt)
- wyznaczyć i narysować gęstość brzegową g(x) (1pkt)
- wyznaczyć i narysować gęstość brzegową h(y) (1pkt)
Uwagi
- Wszystkie wielkości (stałą c, dystrybuantę, gęstości brzegowe) wyznaczamy numerycznie np. wykorzystując metodę
Integral.
- Skrytp powienien być napisany w taki sposób aby wykonywał obliczenia dla dowolnego m i n.
- Należy oznaczyć i podpisać wszystkie osie.
- Funkcje rozkladu gestosci (obiekt TF2) tworzymy poprzez wykorzystanie funkcji jak
poniżej (odpowiednio zdefiniowanej dla wszystkich wartości x i y)
Wynik
Wykresy:
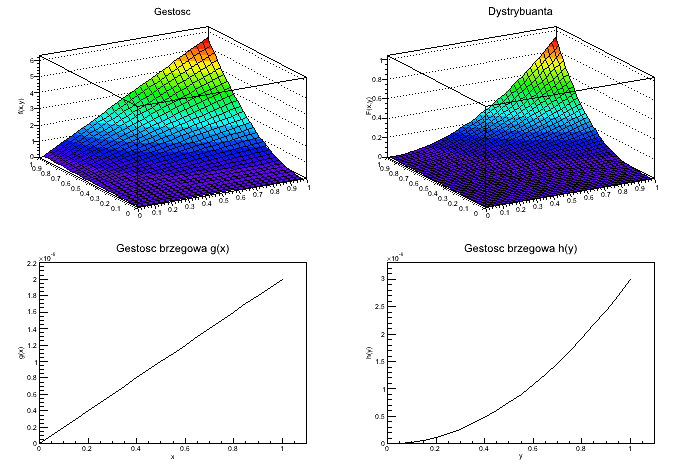
Output:
Wspolczynnik normujacy c=6
