From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 31: |
Line 31: |
| | | | |
| | Output: | | Output: |
| - | Wspolczynnik normujacy c=0.25
| + | E(X)=0.990827 |
| - | E(X)=1.14297 | + | E(Y)=0.990535 |
| - | E(Y)=1.57093 | + | sigma(X)=0.377467 |
| - | sigma(X)=0.754221 | + | sigma(Y)=0.377583 |
| - | sigma(Y)=0.685256 | + | cov(X,Y)=-0.0137694 |
| - | cov(X,Y)=-0.000631452 | + | rho(X,Y)=-0.09661 |
| - | rho(X,Y)=-0.00122177 | + | |
Revision as of 09:44, 21 March 2016
Zadanie
Dana jest gęstość prawdopodobieństwa:
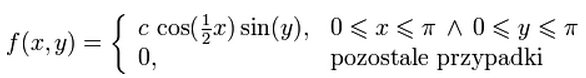
Należy:
- wyznaczyć stałą c w taki sposób aby rozkład gęstości był unormowany
- wylosować z rozkładu gęstości parę liczb (x,y) i następnie wypełnić nimi histogram gęstości prawdopodobieństwa f(x,y) (0.5pkt)
- unormować histogram gęstości prawdopodobieństwa (0.5pkt)
- wyznaczyć i narysować histogram dystrybuanty F(x,y) (1pkt)
- wyznaczyć i narysować histogram gęstości brzegowej g(x) i h(y) (1pkt)
- wyznaczyć:
- wartości oczekiwane: E(X), E(Y) (0.5pkt)
- odchylenia standardowe sigma(X), sigma(Y) (0.5pkt)
- kowariancję cov(X,Y) (0.5pkt)
- współczynnik korelacji rho(X,Y) (0.5pkt)
Uwagi
- Do pracy z histogramami należy wykorzystać obiekty
TH1D i TH2D. Krótki przegląd możliwości tych obiektów można znaleźć w dokumencie: Histograms
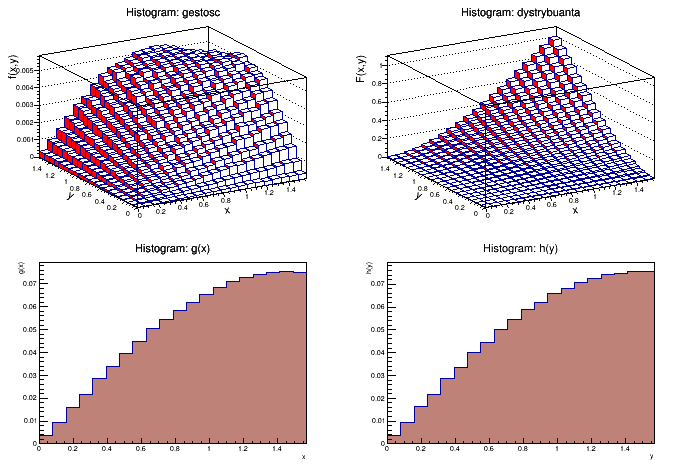
Przykładowy wynik
Wykresy:
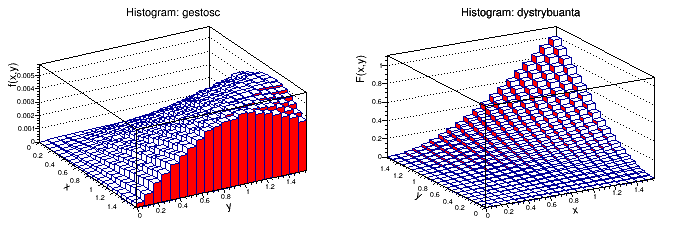
Wykres gęstości obrócony:
Output:
E(X)=0.990827
E(Y)=0.990535
sigma(X)=0.377467
sigma(Y)=0.377583
cov(X,Y)=-0.0137694
rho(X,Y)=-0.09661