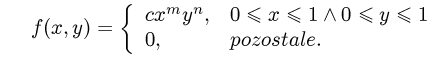KADD 2016 Zadanie 3

From Łukasz Graczykowski

Revision as of 17:05, 13 March 2016 (view source) Lgraczyk (Talk | contribs) (Created page with "==Zadanie== Niech X będzie zmienną losową o gęstości prawdopodobieństwa f(x): File:wzor_lab2.png Należy: * Narysować gęstość prawdopodobieństwa f(x) (0.5 pkt) *...") ← Older edit		Revision as of 17:06, 13 March 2016 (view source) Lgraczyk (Talk | contribs) Newer edit →
Line 1:		Line 1:
-	==Zadanie==	+	{| align="right"
		+	| __TOC__
		+	|}
-	Niech X będzie zmienną losową o gęstości prawdopodobieństwa f(x):
-	[[File:wzor_lab2.png]]
-	Należy:	+	== Zadanie ==
-	* Narysować gęstość prawdopodobieństwa f(x) (0.5 pkt)	+	Dana jest gęstość prawdopodobieństwa:
-	* Narysować dystrybuantę F(x). Dystrybuantę należy obliczyć analitycznie oraz numerycznie (1 pkt)	+
-	* Obliczyć prawdopodobieństwo P(5 <= X \<= 10) (0.5 pkt)	+
-	* Obliczyć wartość oczekiwaną E(X) oraz porównać z wynikiem analitycznym (1 pkt)	+
-	* Obliczyć wariancję V(X) oraz porównać z wynikiem analitycznym (1 pkt)	+
-	* Wyznaczyć mode rozkładu (0.5 pkt)	+
-	* Wyznaczyć kwantyle: (0.5 pkt)	+
-	** kwartyl dolny	+
-	** mediana	+
-	** kwartyl górny	+
-	==Wyniki==	+	[[File:Wzor_Lab03_Kadd2012.png]]
		+
		+	Należy dla parametrów '''m=1''' i '''n=2''':
		+	* wyznaczyć stałą c w taki sposób aby rozkład gęstości był unormowany (1pkt)
		+	* narysować gęstość prawdopodobieństwa f(x,y) (1pkt)
		+	* wyznaczyć i narysować dystrybuante F(x,y) (1pkt)
		+	* wyznaczyć i narysować gęstość brzegową g(x) (1pkt)
		+	* wyznaczyć i narysować gęstość brzegową h(y) (1pkt)
		+
		+	== Uwagi ==
		+	* Wszystkie wielkości (stałą c, dystrybuantę, gęstości brzegowe) wyznaczamy numerycznie np. wykorzystując metodę <code>Integral</code>.
		+	* Skrypt powienien być napisany w taki sposób aby wykonywał obliczenia dla dowolnego m i n.
		+	* Należy oznaczyć i podpisać wszystkie osie.
		+	* Funkcję rozkladu gestosci (obiekt TF2) tworzymy poprzez wykorzystanie konstruktora zawierającego wskaźnik na funkcję (odpowiednio zdefiniowanej dla wszystkich wartości x i y):
		+	double fcn(double *x, double *params)
		+
		+	TF2(const char* name, void* fcn, Double_t xmin = 0, Double_t xmax = 1, Double_t ymin = 0, Double_t ymax = 1, Int_t npar = 0)
		+
		+	Przykład:
		+	double function(double *x, double *params)
		+	{
		+	if(x[0]>=0 && x[1]>=0)
		+	return params[0]*x[0]*x[1];
		+	return 0;
		+	}
		+	...
		+	double xmin = 0;
		+	double xmax = 10;
		+	double ymin = 0;
		+	double xmax = 10;
		+	int nparams = 1;
		+	TF2 * fun1 = new TF2("fun1",function,xmin,xmax,ymin,ymax,nparams);
		+
		+	== Wynik ==
	Wykresy:		Wykresy:
-	[[File:lab2_3.png]]	+	[[File:Zad03_KADD2012.png]]
	Output:		Output:
-	P(5<X<10) z gestosci: 0.245723	+	Wspolczynnik normujacy c=6
-	P(5<X<10) z dystrybuanty: 0.245723	+
-	Srednia z funkcji TF1: 5.98798	+
-	Srednia analitycznie: 6	+
-	Wariancja z funkcji TF1: 35.3988	+
-	Wariancja analitycznie: 36	+
-	Moda: 0	+
-	x0.25: 1.74	+
-	x0.5: 4.16	+
-	x0.75: 8.32	+

---

Revision as of 17:06, 13 March 2016

Contents 1 Zadanie 2 Uwagi 3 Wynik

Zadanie

Dana jest gęstość prawdopodobieństwa:

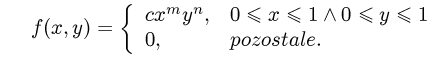
Należy dla parametrów m=1 i n=2:

• wyznaczyć stałą c w taki sposób aby rozkład gęstości był unormowany (1pkt)
• narysować gęstość prawdopodobieństwa f(x,y) (1pkt)
• wyznaczyć i narysować dystrybuante F(x,y) (1pkt)
• wyznaczyć i narysować gęstość brzegową g(x) (1pkt)
• wyznaczyć i narysować gęstość brzegową h(y) (1pkt)

Uwagi

• Wszystkie wielkości (stałą c, dystrybuantę, gęstości brzegowe) wyznaczamy numerycznie np. wykorzystując metodę Integral.
• Skrypt powienien być napisany w taki sposób aby wykonywał obliczenia dla dowolnego m i n.
• Należy oznaczyć i podpisać wszystkie osie.
• Funkcję rozkladu gestosci (obiekt TF2) tworzymy poprzez wykorzystanie konstruktora zawierającego wskaźnik na funkcję (odpowiednio zdefiniowanej dla wszystkich wartości x i y):

double fcn(double *x, double *params)

TF2(const char* name, void* fcn, Double_t xmin = 0, Double_t xmax = 1, Double_t ymin = 0, Double_t ymax = 1, Int_t npar = 0)

Przykład:

double function(double *x, double *params)
{
   if(x[0]>=0 && x[1]>=0)
     return params[0]*x[0]*x[1];
   return 0;
}
...
double xmin = 0;
double xmax = 10;
double ymin = 0;
double xmax = 10;
int nparams = 1;
TF2 * fun1 = new TF2("fun1",function,xmin,xmax,ymin,ymax,nparams);

Wynik

Wykresy:

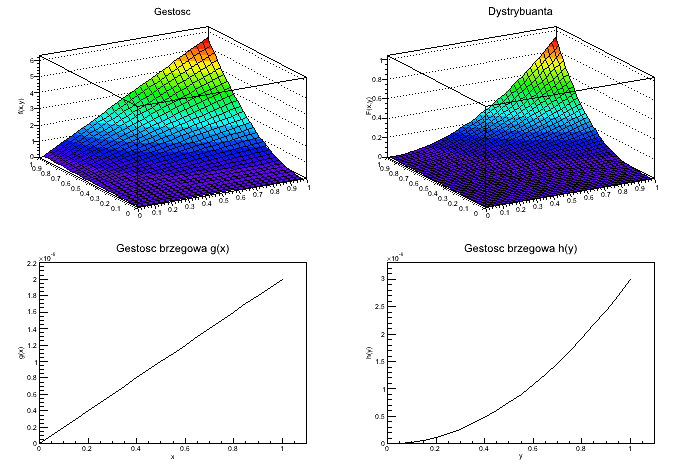
Output:

Wspolczynnik normujacy c=6