From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 1: |
Line 1: |
| | == Zadanie == | | == Zadanie == |
| | + | ''Część pierwsza'': '''Rozkład chi-kwadrat''' (3 pkt.) |
| | + | |
| | + | Napisać skrypt rysujący wykres rozkładu chi-kwadrat oraz jego dystrybuanty dla różnych wartości liczby stopni swobody: <code>n=1..20</code>. |
| | + | Uwagi: |
| | + | * Proszę wykorzystać w zadaniu obiekty klasy TH1D. |
| | + | * Dystrybunatę należy obliczyć numerycznie. |
| | + | |
| | + | ''Część druga'': '''Dopasowanie funkcji Gaussa''' (2 pkt.) |
| | + | |
| | + | Napisać skrypt dokonujący splotu n rozkładów jednostajnych. Liczbę n należy wyznaczyć jako najmniejszą liczbę dodanych rozkładów, dla której wartość chi2/ndf, obliczona na podstawie dopasowania funkcji Gaussa (wykorzystując gotowe funkcje klasy TF1) jest mniejsza od 1.0. |
| | + | |
| | + | == Wynik == |
| | + | '''Rozkład chi-kwadrat''' |
| | + | |
| | + | [[File:lab9.png]] |
| | + | |
| | + | '''Dopasowanie funkcji Gaussa''' |
| | + | |
| | + | [[File:lab9_splot.png]] |
| | + | |
| | + | Output (przykładowy): |
| | + | liczba splecionych rozkladow jednostajnych = 9 |
| | + | chi2/ndf = 55.724/59 = 0.944475 |
Revision as of 10:23, 7 May 2012
Zadanie
Część pierwsza: Rozkład chi-kwadrat (3 pkt.)
Napisać skrypt rysujący wykres rozkładu chi-kwadrat oraz jego dystrybuanty dla różnych wartości liczby stopni swobody: n=1..20.
Uwagi:
- Proszę wykorzystać w zadaniu obiekty klasy TH1D.
- Dystrybunatę należy obliczyć numerycznie.
Część druga: Dopasowanie funkcji Gaussa (2 pkt.)
Napisać skrypt dokonujący splotu n rozkładów jednostajnych. Liczbę n należy wyznaczyć jako najmniejszą liczbę dodanych rozkładów, dla której wartość chi2/ndf, obliczona na podstawie dopasowania funkcji Gaussa (wykorzystując gotowe funkcje klasy TF1) jest mniejsza od 1.0.
Wynik
Rozkład chi-kwadrat
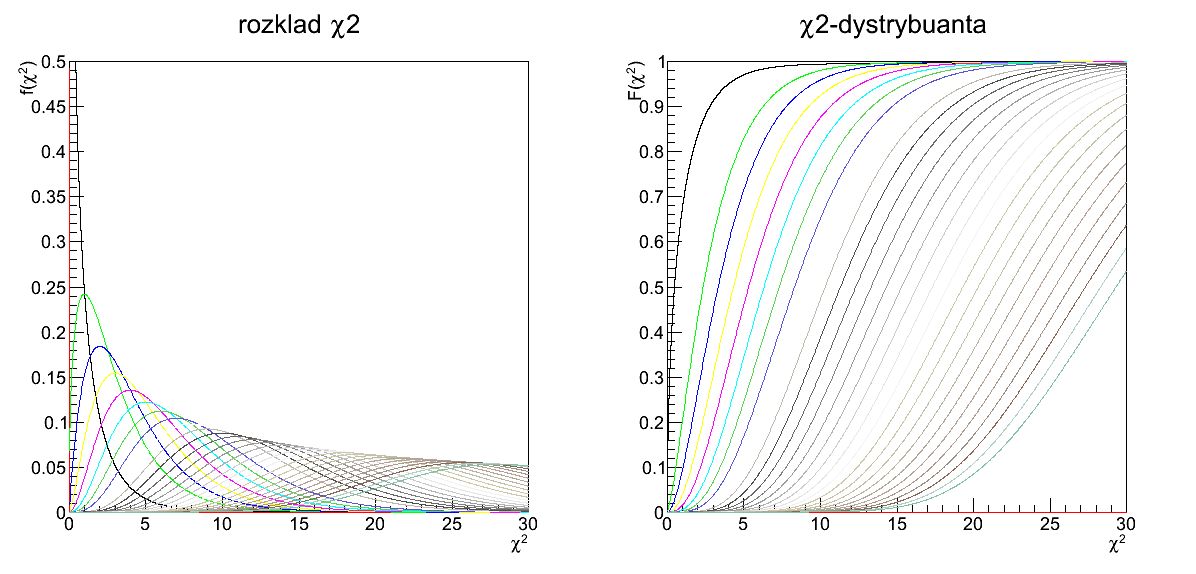
Dopasowanie funkcji Gaussa
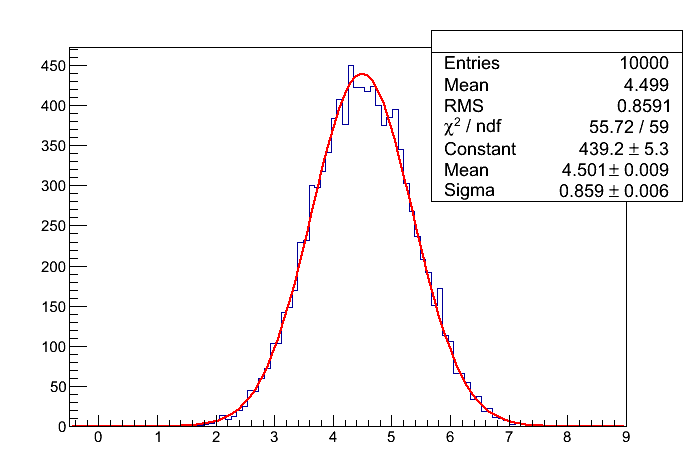
Output (przykładowy):
liczba splecionych rozkladow jednostajnych = 9
chi2/ndf = 55.724/59 = 0.944475

