KADD 2012 Zadanie 7

From Łukasz Graczykowski

Revision as of 16:35, 1 April 2012 (view source) Lgraczyk (Talk | contribs) (→Zadanie) ← Older edit		Revision as of 16:35, 1 April 2012 (view source) Lgraczyk (Talk | contribs) (→Wynik) Newer edit →
Line 32:		Line 32:
	Output:		Output:
	Liczba Pi wynosi: 3.14392		Liczba Pi wynosi: 3.14392
		+
		+	''Część druga''

---

Revision as of 16:35, 1 April 2012

Contents 1 Zadanie 2 Wynik

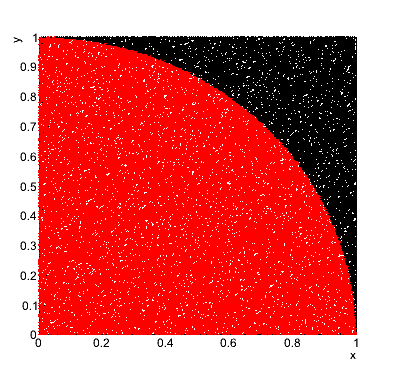
Zadanie

Część pierwsza: obliczanie liczby Pi (1 pkt.)

Należy napisać funkcję, która oblicza liczbę Pi metodą von Neumanna (jest to bodajże najprostszy przykład wykorzystania metody typu Monte Carlo). W tym celu losujemy z rozkładu jednorodnego na przedziale [0,1] dwie liczby x i y, i sprawdzamy, czy wylosowana para mieści się wewnątrz koła o promieniu 1. Następnie używając stosunku par zaakceptowanych (mieszczących się wewnątrz) do odrzuconych (tych, które leżą poza okręgiem) oraz wzoru na pole koła, należy obliczyć liczbę Pi. Ponadto, należy narysować wykres trafień leżących wewnątrz oraz na zewnątrz koła:

• stworzyć dwa obiekty typu TGraph i jeden z nich wypełniać zaakceptowanymi parami (x,y)>, drugi zaś odrzuconymi. Oba wykresy narysować na jednym panelu,
• dodatkowo można stworzyć obiekt TH1D i wypełnić go zaakceptowanymi wartościami x.

Część druga: generowanie liczb pseudolosowych z dowolnego rozkładu metodą akceptacji i odrzucania von Neumanna (2 pkt.)

Wykorzystana tydzień temu metoda transformacji rozkładu jednorodnego z wykorzystaniem funkcji odwrotnej do dystrybuanty ma ograniczone zastosowanie. Jej zastosowanie jest możliwe tylko wtedy, gdy znana jest jawna postać dystrybuanty oraz można znaleźć funkcję do niej odwrotną. Metoda von Neumanna pozwala wygenerowanie liczb pseudolosowych, gdy znany jest tylko rozkład g(y).

Należy stworzyć trzy bardzo podobne funkcje przyjmujące obiekt typu TF1. Powinny one przyjmować funkcję g na przedziale [min,max]:

• double losujVonNeumann(TF1 *g, double min, double max) - funkcja zwraca jedną liczbę pseudolosową z rozkładu danego przez funkcję gęstości prawdopodobieństwa g,
• double wydajnoscVonNeumann(TF1 *g, double min, double max, int n) - funkcja zwraca wydajność metody akceptacji i odrzucania von Neumanna dla zadanej liczby losowań n,
• double calkaVonNeumann(TF1 *g, double min, double max, int n) - funkcja zwraca całkę oznaczoną (pole powierzchni pod krzywą) z gęstości g na przedzialne [min,max].

Część trzecia: metoda akceptacji i odrzucania von Neumanna z funkcją pomocniczą

Wynik

Część pierwsza

Output:

 Liczba Pi wynosi: 3.14392

Część druga