From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 8: |
Line 8: |
| | | | |
| | == Zadanie == | | == Zadanie == |
| - |
| |
| | ''Część pierwsza'': '''Obliczanie liczby Pi''' (1 pkt.) | | ''Część pierwsza'': '''Obliczanie liczby Pi''' (1 pkt.) |
| | | | |
| | Należy napisać '''funkcję''', która oblicza liczbę Pi '''metodą Monte Carlo'''. W tym celu losujemy z rozkładu jednorodnego na przedziale [0,1] dwie liczby x i y, i sprawdzamy, czy wylosowana para mieści się wewnątrz koła o promieniu 1. Następnie używając stosunku par zaakceptowanych (mieszczących się wewnątrz) do odrzuconych (tych, które leżą poza okręgiem) oraz wzoru na pole koła, należy obliczyć liczbę Pi. Ponadto, należy narysować wykres trafień leżących wewnątrz oraz na zewnątrz koła. | | Należy napisać '''funkcję''', która oblicza liczbę Pi '''metodą Monte Carlo'''. W tym celu losujemy z rozkładu jednorodnego na przedziale [0,1] dwie liczby x i y, i sprawdzamy, czy wylosowana para mieści się wewnątrz koła o promieniu 1. Następnie używając stosunku par zaakceptowanych (mieszczących się wewnątrz) do odrzuconych (tych, które leżą poza okręgiem) oraz wzoru na pole koła, należy obliczyć liczbę Pi. Ponadto, należy narysować wykres trafień leżących wewnątrz oraz na zewnątrz koła. |
| | + | |
| | + | ''Część druga'': '''Generowanie liczb pseudolosowych z dowolnego rozkładu metodą von Neumanna''' |
| | + | |
| | + | |
| | + | == Wynik == |
| | + | ''Część pierwsza'' |
| | + | |
| | | | |
| | Przykładowy wynik: | | Przykładowy wynik: |
| Line 19: |
Line 25: |
| | Output: | | Output: |
| | Liczba Pi wynosi: 3.14392 | | Liczba Pi wynosi: 3.14392 |
| - |
| |
| - | ''Część druga'': '''Generowanie liczb pseudolosowych z dowolnego rozkładu metodą von Neumanna'''
| |
Revision as of 16:06, 1 April 2012
Zadanie
Część pierwsza: Obliczanie liczby Pi (1 pkt.)
Należy napisać funkcję, która oblicza liczbę Pi metodą Monte Carlo. W tym celu losujemy z rozkładu jednorodnego na przedziale [0,1] dwie liczby x i y, i sprawdzamy, czy wylosowana para mieści się wewnątrz koła o promieniu 1. Następnie używając stosunku par zaakceptowanych (mieszczących się wewnątrz) do odrzuconych (tych, które leżą poza okręgiem) oraz wzoru na pole koła, należy obliczyć liczbę Pi. Ponadto, należy narysować wykres trafień leżących wewnątrz oraz na zewnątrz koła.
Część druga: Generowanie liczb pseudolosowych z dowolnego rozkładu metodą von Neumanna
Wynik
Część pierwsza
Przykładowy wynik:
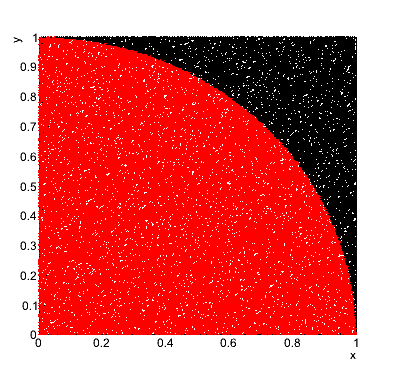
Output:
Liczba Pi wynosi: 3.14392
