From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 42: |
Line 42: |
| | X1=3.00691+/-0.495242 | | X1=3.00691+/-0.495242 |
| | X2=2.00581+/-0.40909 | | X2=2.00581+/-0.40909 |
| - | X3=9.87815+/-1.88409 | + | X3=9.97287+/-1.98102 |
| | rho(X1,X2)=0.156132 | | rho(X1,X2)=0.156132 |
| - | rho(X1,X3)=-0.0105487 | + | rho(X1,X3)=-0.00698853 |
| - | rho(X2,X3)=0.00365763 | + | rho(X2,X3)=0.00875851 |
| | | | |
| | To jest macierz kowariancji wielkosci X | | To jest macierz kowariancji wielkosci X |
| | 3x3 matrix is as follows | | 3x3 matrix is as follows |
| - |
| + | |
| | | 0 | 1 | 2 | | | | 0 | 1 | 2 | |
| - | --------------------------------------------
| + | -------------------------------------------- |
| - | 0 | 0.4952 0.0316 -0.009837 | + | 0 | 0.4952 0.0316 -0.006855 |
| - | 1 | 0.0316 0.4091 0.002823 | + | 1 | 0.0316 0.4091 0.0071 |
| - | 2 | -0.009837 0.002823 1.884 | + | 2 | -0.006855 0.0071 1.981 |
| | | | |
| | | | |
| | To jest macierz kowariancji wielkosci Y | | To jest macierz kowariancji wielkosci Y |
| | 2x2 matrix is as follows | | 2x2 matrix is as follows |
| - |
| + | |
| - | | 0 | 1 |
| + | | 0 | 1 | |
| - | -------------------------------
| + | ------------------------------- |
| - | 0 | 14.71 9.015 | + | 0 | 14.86 9.034 |
| - | 1 | 9.015 6.796 | + | 1 | 9.034 6.796 |
| - |
| + | |
| - | Y1=25.921+/-14.7131 | + | Y1=26.0157+/-14.8647 |
| | Y2=12.5267+/-6.79564 | | Y2=12.5267+/-6.79564 |
| - | rho(Y1,Y2)=0.901585 | + | rho(Y1,Y2)=0.898826 |
| - | rho(Y2,Y1)=0.901585 | + | rho(Y2,Y1)=0.898826 |
Revision as of 09:13, 19 March 2012
Zadanie
Wykonano pomiary trzech wielkości fizycznych X1, X2 oraz X2. Wyniki pomiarów znajdują się w plikach: dane1.dat, dane2.dat oraz dane3.dat.
- Należy określić wynik pomiaru (średnia oraz niepewność - odchylenie standardowe) obu tych wielkości oraz narysować wykresy zależności między zmiennymi
(X1, X2), (X2, X3) oraz (X1, X3). (1 pkt)
Wielkości fizyczne Y1, Y2 związane są z wielkościami X1, X2, X3 następującymi relacjami:
Y1 = 2 X1 + 5 X2 + X3
Y2 = 3 + 0.5 X1 + 4 X2
Należy wyznaczyć:
- macierz kowariancji zmiennych X1, X2, X3 (1 pkt)
- zmierzone wartości średnie zmiennych Y1, Y2 w pomiarze pośrednim (0.5 pkt)
- macierz kowariancji zmiennych Y1, Y2 (1pkt)
- błędy z jakimi zmierzono pośrednio wielkości Y1, Y2 (1 pkt)
- wpółczynnik korelacji pomiędzy zmiennymi Y1 i Y2 (0.5 pkt)
Uwagi
- Wczytywanie danych z pliku (tak samo jak w języku C++):
ifstream ifile;
ifile.open("dane.dat");
double val;
while(infile>>val)
{
cout<<val<<endl;
}
ifile.close();
- Do wszystkich operacji na macierzach (tworzenie macierzy kowariancji, mnożenie macierzy, transponowanie macierzy) - polecana jest klasa
TMatrixD
Wynik
Wykresy:
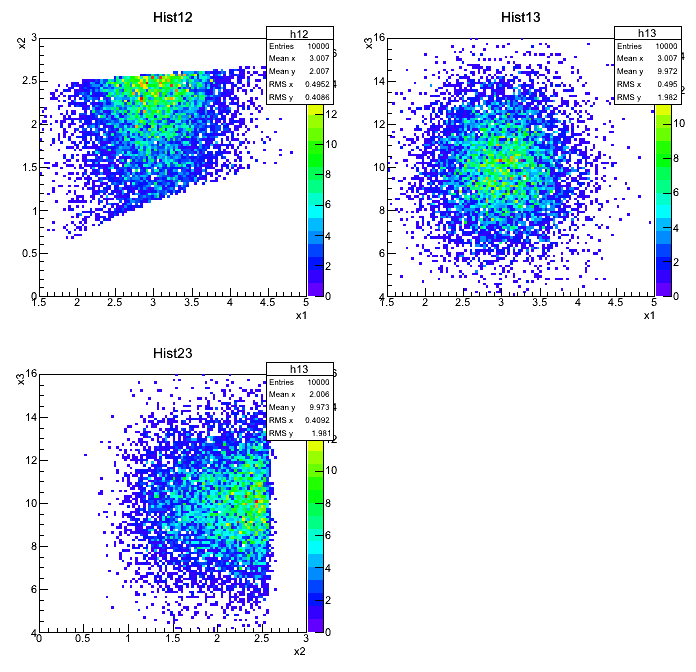
Output:
X1=3.00691+/-0.495242
X2=2.00581+/-0.40909
X3=9.97287+/-1.98102
rho(X1,X2)=0.156132
rho(X1,X3)=-0.00698853
rho(X2,X3)=0.00875851
To jest macierz kowariancji wielkosci X
3x3 matrix is as follows
| 0 | 1 | 2 |
--------------------------------------------
0 | 0.4952 0.0316 -0.006855
1 | 0.0316 0.4091 0.0071
2 | -0.006855 0.0071 1.981
To jest macierz kowariancji wielkosci Y
2x2 matrix is as follows
| 0 | 1 |
-------------------------------
0 | 14.86 9.034
1 | 9.034 6.796
Y1=26.0157+/-14.8647
Y2=12.5267+/-6.79564
rho(Y1,Y2)=0.898826
rho(Y2,Y1)=0.898826
