From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 7: |
Line 7: |
| | |} | | |} |
| | | | |
| - | <!--
| |
| | == Zadanie == | | == Zadanie == |
| | ''Część pierwsza'': '''sploty funkcji''' (3 pkt.) | | ''Część pierwsza'': '''sploty funkcji''' (3 pkt.) |
| Line 60: |
Line 59: |
| | | | |
| | [[File:galton.png]] | | [[File:galton.png]] |
| - |
| |
| - | -->
| |
Latest revision as of 11:13, 11 April 2022
Zadanie
Część pierwsza: sploty funkcji (3 pkt.)
Jako zadanie należy zaimplementować funkcję wykonującą splot n zadanych rozkładów:
// f - tablica wskaznikow do obiektow TF1, rozklady skladowe
// k - wymiar tablicy f
// h - histogram do ktorego wrzucamy wynik splotu
// n - liczba losowan
void splot(TF1 **f, int k, TH1D *h, int n);
Zadane rozkłady reprezentowane są przez obiekty TF1. Wynik splotu reprezentowany jest przez obiekt TH1D.
Następnie należy:
- wykonać i narysować splot dwóch rozkładów jednorodnych U(0.0,2.0) i U(0.0,2.0), po czym dodać do splotu jeszcze trzeci rozkład jednorodny U(0.0,2.0) i splot wszystkich 3 rozkładów narysować (losujemy liczby z rozkładów wchodzących jako elementy splotu i dodajemy je do siebie, powtarzamy to wielokrotnie i wrzucamy do histogramu - wyjściowy histogram to splot rozkładów wejściowych),
- wykonać i narysować splot dwóch rozkładów normalnych N(1.0,0.2), N(3.0,0.5) oraz policzyć średnią i odchylenie standardowe powstałego rozkładu (należy wypisać średnie i odchylenia rozkładów wejściowych oraz splotu).
Część druga: tablica Galtona (2 pkt.)
Jako zadanie należy napisać skrypt symulujący deskę Galtona. Parametrami skryptu powinny być:
-
n - liczba prób (kul)
-
l - liczba rzędów
-
p - prawdopodobieństwo ruchu kuli w prawo (sukcesu)
Dla zadanych wartości parametrów skryptu należy narysować histogram rozkładu kul otrzymany w wyniku symulacji oraz przewidywanie teoretyczne. Symulację wykonujemy dla 3 różnych zestawów parametrów dobranych w taki sposób aby otrzymać rozkład dwumianowy.
W ramach zadania należy:
- zaimplementować funkcję symulującą deskę Galtona np:
void deskaGaltona(TH1D * h, int n, int l, double p);
- dobrać parametry
n i p w taki sposób aby otrzymać rozkład dwumianowy.
Uwagi
- Czytamy dokładnie Wykład 7 link o splotach - slajdy 14-26, slajd 13 o centralnym twierdzeniu granicznym (CTG) też warto zapamiętać
- Zgodnie ze slajdem 17, jeżeli mamy zmienną losową U=X+Y, gdzie X i Y to zmienne losowe opisane rozkładami f(x) oraz f(y), to rozkład f(u) zmiennej losowej U jest splotem rozkładów f(x) zmiennej X oraz f(y) zmiennej Y - zrobienie splotu przy losowaniu zmiennych losowych z rozkładów wejściowych (jak w tym zadaniu) to zatem nic innego jak dodawanie do siebe tych wartości i wynikiem jest histogram - rozkład takiej sumy, który jest splotem rozkładów wejściowych
Wynik
Część pierwsza: sploty funkcji
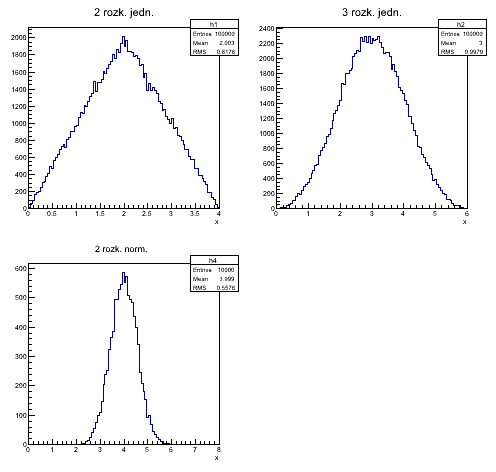
Output:
EX 1: 1
EX 2: 3
EX: 4.00079
VX 1: 0.04
VX 2: 0.25
VX: 0.314075
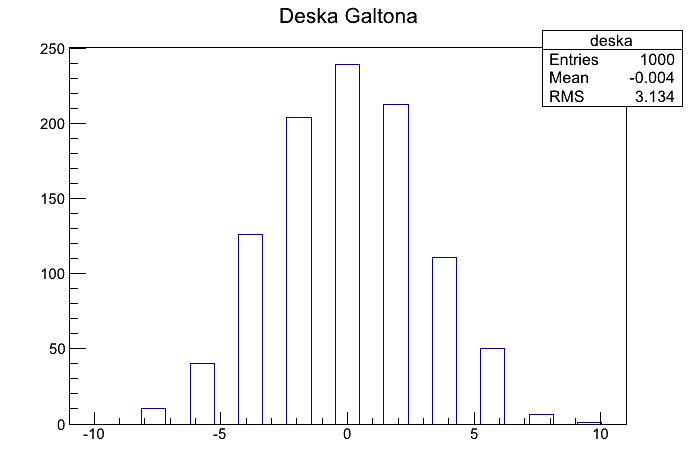
Część druga: tablica Galtona