From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 1: |
Line 1: |
| - | == Zadanie ==
| |
| - | '''Weryfikacja hipotez statystycznych''' (5 pkt.)
| |
| - |
| |
| - | * Przeprowadzono eksperyment naświetlania wodorowej komory pęcherzykowej wiązką fotonów w celu badania oddziaływań fotonów z protonami. Fotony powodują powstawanie par elektron-pozyton, które mogą być wykorzystane do monitorowania wiązki fotonów. Częstość występowania zdjęć z 0,1,2,... parami elektron-pozyton powinna podlegać rozkładowi Poissona. Należy wczytać dane z [http://hirg.if.pw.edu.pl/~mszymanski/kadd/dane.txt pliku] (w pierwszej kolumnie znajduje się liczba par elektronowych na zdjęciu <code>k</code>, a w drugiej liczba zdjęć zawierających <code>k</code> par elektronowych) i dopasować do nich funkcję Poissona. (1 pkt.)
| |
| - |
| |
| - | * Narysować na jednym wykresie punkty pomiarowe i dopasowanie. (1 pkt.)
| |
| - |
| |
| - | * Sprawdzić jakość dopasowania za pomocą testu χ2. W tym celu należy zaimplementować funkcję obliczającą statystykę testową χ2 zgodnie z wzorem [[File:wzor.png]]
| |
| - | gdzie: nk - liczba obserwacji w k-tym binie, npk - przewidywana przez teorię liczba przypadków w k-tym binie tj.:
| |
| - |
| |
| - | // h - histogram danych
| |
| - | // g - przewidywanie "teoretyczne"
| |
| - | double chi2(TH1D *h, TF1 *f);
| |
| - |
| |
| - | * Okreslić liczbę stopni swobody i obliczyć wartość statystyki testowej. (1 pkt.)
| |
| - |
| |
| - | * Zaimplementować funkcję zwracającą wynik testu χ2 na zadanym poziomie istotności α tj.:
| |
| - | // 1 - brak podstaw do odrzucenia hipotezy
| |
| - | // 0 - sa podstawy do odrzucenia hipotezy
| |
| - | // Parametry:
| |
| - | // T - wartosc statystyki testowej chi2
| |
| - | // alpha - poziom istotnosci
| |
| - | // ndf - liczba stopni swobody rozkladu chi2
| |
| - | int testChi2(double T, double alpha, int ndf);
| |
| - |
| |
| - | Wykorzystując zaimplementowaną funkcję zweryfikować hipotezę mówiacą, że dane pomiarowe podlegają rozkładowi Poissona. Dobrać odpowiednią wartość poziomu istotności. Podać wartość krytczną testu oraz jego wynik. (2 pkt.)
| |
| - |
| |
| | == Wynik == | | == Wynik == |
| | | | |
Revision as of 08:07, 11 May 2012
Wynik
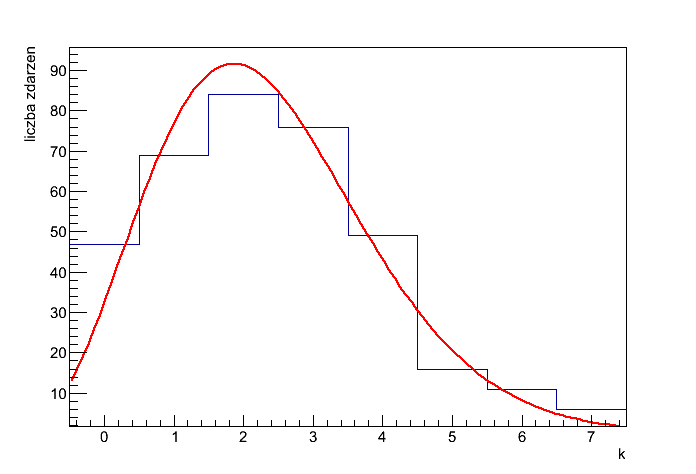
Output:
wartosc statystyki testowej = 11.1406
Liczba stopni swobody = 6
Wartosc krytyczna = 16.8119
Poziom istotnosci = 0.01
Wynik testu: brak podstaw do odrzucenia hipotezy
