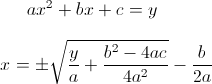From Łukasz Graczykowski
(Difference between revisions)
|
|
| (17 intermediate revisions not shown) |
| Line 8: |
Line 8: |
| | | | |
| | == Zadanie == | | == Zadanie == |
| | + | ''Część pierwsza'': '''obliczanie liczby Pi''' (1 pkt.) |
| | | | |
| - | ''Część pierwsza'': '''Obliczanie liczby Pi''' (1 pkt.) | + | Należy napisać '''funkcję''', która oblicza liczbę Pi '''metodą von Neumanna''' (jest to bodajże najprostszy przykład wykorzystania metody typu '''Monte Carlo'''). W tym celu losujemy z rozkładu jednorodnego na przedziale [0,1] dwie liczby x i y, i sprawdzamy, czy wylosowana para mieści się wewnątrz koła o promieniu 1. Następnie używając stosunku par zaakceptowanych (mieszczących się wewnątrz) do odrzuconych (tych, które leżą poza okręgiem) oraz wzoru na pole koła, należy obliczyć liczbę Pi. Ponadto, należy narysować wykres trafień leżących wewnątrz oraz na zewnątrz koła: |
| | + | * stworzyć dwa obiekty typu <code>TGraph</code> i jeden z nich wypełniać zaakceptowanymi parami (x,y), drugi zaś odrzuconymi. Oba wykresy narysować na jednym panelu, |
| | + | * dodatkowo można stworzyć obiekt <code>TH1D</code> i wypełnić go zaakceptowanymi wartościami x. Będzie dany rozkładem wyznaczonym ze wzoru na pole koła. |
| | | | |
| - | Należy napisać '''funkcję''', która oblicza liczbę Pi '''metodą Monte Carlo'''. W tym celu losujemy z rozkładu jednorodnego na przedziale [0,1] dwie liczby x i y, i sprawdzamy, czy wylosowana para mieści się wewnątrz koła o promieniu 1. Następnie używając stosunku par zaakceptowanych (mieszczących się wewnątrz) do odrzuconych (tych, które leżą poza okręgiem) oraz wzoru na pole koła, należy obliczyć liczbę Pi. Ponadto, należy narysować wykres trafień leżących wewnątrz oraz na zewnątrz koła.
| + | ''Część druga'': '''generowanie liczb pseudolosowych z dowolnego rozkładu metodą akceptacji i odrzucania von Neumanna''' (3 pkt.) |
| | | | |
| - | Przykładowy wynik:
| + | Wykorzystana tydzień temu metoda transformacji rozkładu jednorodnego z wykorzystaniem funkcji odwrotnej do dystrybuanty ma ograniczone zastosowanie. Jej zastosowanie jest możliwe tylko wtedy, gdy znana jest jawna postać dystrybuanty oraz można znaleźć funkcję do niej odwrotną. '''Metoda von Neumanna''' pozwala wygenerowanie liczb pseudolosowych, gdy znany jest tylko rozkład g(y). W ogólności metoda działa nawet wtedy, gdy funkcja g(y) ''nie jest'' rozkładem gęstości prawdopodobieństwa (całka z niej nie wynosi 1). Pozwala to na bardzo szerokie wykorzystanie metody von Neumanna - przede wszystkim do obliczania całek oznaczonych ze skomplikowanych funkcji, gdy ich analityczne scałkowanie jest niemożliwe. Metody tego typu noszą nazwę wspomnianych wcześniej '''metod Monte Carlo'''. |
| | + | |
| | + | Należy stworzyć trzy '''bardzo podobne''' funkcje przyjmujące obiekt typu <code>TF1</code>. Powinny one przyjmować funkcję g na przedziale [min,max]: |
| | + | * <code>double losujVonNeumann(TF1 *g, double min, double max)</code> - funkcja zwraca ''jedną'' liczbę pseudolosową z funkcji g(y), |
| | + | * <code>double wydajnoscVonNeumann(TF1 *g, double min, double max, int n)</code> - funkcja zwraca wydajność metody akceptacji i odrzucania von Neumanna dla danej funkcji g(y) oraz zadanej liczby losowań n, |
| | + | * <code>double calkaVonNeumann(TF1 *g, double min, double max, int n)</code> - funkcja zwraca całkę oznaczoną (pole powierzchni pod krzywą) z funkcji g(y) na przedzialne [min,max] przy liczbie losowań n. |
| | + | |
| | + | ''Część trzecia:'' '''metoda akceptacji i odrzucania von Neumanna z funkcją pomocniczą''' (1 pkt.) |
| | + | |
| | + | W celu zwiększenia wydajności metody von Neumanna, można posłużyć się ograniczeniem przedziału losowania w postacji zadanej funkcji pomocniczej. W tej części zaimplementować funkcję, która oblicza całkę z funkcji g(y) metodą akceptacji i odrzucania von Neumanna z funkcją pomocniczą s(y): |
| | + | * <code>double calkaVonNeumannZPomoc(TF1 *g, TF1 *s, double min, double max, int n, double &wydajnosc)</code> - zwraca całkę na przedziale [min,max] oraz dla zadanej liczby losowań n. Ponadto, funkcja powinna zwrócić '''przez referencję''' (ponieważ w języku C/C++ funkcja nie może zwrócić dwóch wartości) wydajność tej metody. |
| | + | |
| | + | Funkcję s(y) dobieramy tak, by '''zawsze''' znajdowała się powyżej funkcji g(y) i można z niej było łatwo wygenerować liczbę pseudolosową (na przykład metodą transformacji rozkładu jednorodnego z wykorzystaniem odwrotności dystrybuanty; na wykładzie przykład z funkcją liniową). |
| | + | |
| | + | Wszystkie obliczenia należy wykonać dla funkcji typu: |
| | + | [[File:Lab07_funkcja2.png]] |
| | + | |
| | + | == Uwagi == |
| | + | * Funkcja kwadratowa i jej odwrotność: |
| | + | |
| | + | [[File:Odwracanie_kwadratowej.png]] |
| | + | * [http://pl.wikipedia.org/wiki/Metoda_Monte_Carlo Metoda Monte Carlo] - Wikipedia. |
| | + | * [http://www.if.pw.edu.pl/~kisiel/kadd/Wyklad5.pdf Wykład 5] z KADD dr hab. inż. Adama Kisiela. |
| | + | |
| | + | == Wynik == |
| | + | ''Część pierwsza'' |
| | | | |
| | [[File:lab07_kolo2.png]] | | [[File:lab07_kolo2.png]] |
| Line 20: |
Line 48: |
| | Liczba Pi wynosi: 3.14392 | | Liczba Pi wynosi: 3.14392 |
| | | | |
| - | ''Część druga'': '''Generowanie liczb pseudolosowych z dowolnego rozkładu metodą von Neumanna''' | + | ''Części druga i trzecia'' |
| | + | |
| | + | [[File:Lab07_dist.png]] |
| | + | |
| | + | Output: |
| | + | Calka: 0.199 |
| | + | Wydajnosc: 0.2072 |
| | + | Calka (metoda z funkcja pomocnicza): 0.198745 |
| | + | Wydajnosc (metoda z funkcja pomocnicza): 0.39749 |
| | + | Calka liczona metoda Integral: 0.198652 |
Latest revision as of 07:53, 2 April 2012
Zadanie
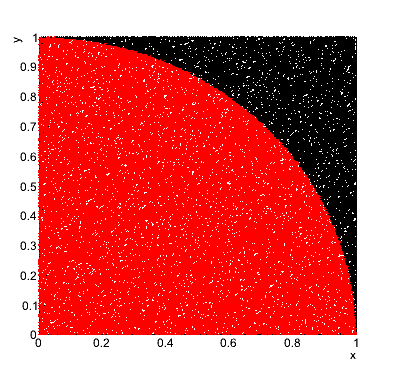
Część pierwsza: obliczanie liczby Pi (1 pkt.)
Należy napisać funkcję, która oblicza liczbę Pi metodą von Neumanna (jest to bodajże najprostszy przykład wykorzystania metody typu Monte Carlo). W tym celu losujemy z rozkładu jednorodnego na przedziale [0,1] dwie liczby x i y, i sprawdzamy, czy wylosowana para mieści się wewnątrz koła o promieniu 1. Następnie używając stosunku par zaakceptowanych (mieszczących się wewnątrz) do odrzuconych (tych, które leżą poza okręgiem) oraz wzoru na pole koła, należy obliczyć liczbę Pi. Ponadto, należy narysować wykres trafień leżących wewnątrz oraz na zewnątrz koła:
- stworzyć dwa obiekty typu
TGraph i jeden z nich wypełniać zaakceptowanymi parami (x,y), drugi zaś odrzuconymi. Oba wykresy narysować na jednym panelu,
- dodatkowo można stworzyć obiekt
TH1D i wypełnić go zaakceptowanymi wartościami x. Będzie dany rozkładem wyznaczonym ze wzoru na pole koła.
Część druga: generowanie liczb pseudolosowych z dowolnego rozkładu metodą akceptacji i odrzucania von Neumanna (3 pkt.)
Wykorzystana tydzień temu metoda transformacji rozkładu jednorodnego z wykorzystaniem funkcji odwrotnej do dystrybuanty ma ograniczone zastosowanie. Jej zastosowanie jest możliwe tylko wtedy, gdy znana jest jawna postać dystrybuanty oraz można znaleźć funkcję do niej odwrotną. Metoda von Neumanna pozwala wygenerowanie liczb pseudolosowych, gdy znany jest tylko rozkład g(y). W ogólności metoda działa nawet wtedy, gdy funkcja g(y) nie jest rozkładem gęstości prawdopodobieństwa (całka z niej nie wynosi 1). Pozwala to na bardzo szerokie wykorzystanie metody von Neumanna - przede wszystkim do obliczania całek oznaczonych ze skomplikowanych funkcji, gdy ich analityczne scałkowanie jest niemożliwe. Metody tego typu noszą nazwę wspomnianych wcześniej metod Monte Carlo.
Należy stworzyć trzy bardzo podobne funkcje przyjmujące obiekt typu TF1. Powinny one przyjmować funkcję g na przedziale [min,max]:
-
double losujVonNeumann(TF1 *g, double min, double max) - funkcja zwraca jedną liczbę pseudolosową z funkcji g(y),
-
double wydajnoscVonNeumann(TF1 *g, double min, double max, int n) - funkcja zwraca wydajność metody akceptacji i odrzucania von Neumanna dla danej funkcji g(y) oraz zadanej liczby losowań n,
-
double calkaVonNeumann(TF1 *g, double min, double max, int n) - funkcja zwraca całkę oznaczoną (pole powierzchni pod krzywą) z funkcji g(y) na przedzialne [min,max] przy liczbie losowań n.
Część trzecia: metoda akceptacji i odrzucania von Neumanna z funkcją pomocniczą (1 pkt.)
W celu zwiększenia wydajności metody von Neumanna, można posłużyć się ograniczeniem przedziału losowania w postacji zadanej funkcji pomocniczej. W tej części zaimplementować funkcję, która oblicza całkę z funkcji g(y) metodą akceptacji i odrzucania von Neumanna z funkcją pomocniczą s(y):
-
double calkaVonNeumannZPomoc(TF1 *g, TF1 *s, double min, double max, int n, double &wydajnosc) - zwraca całkę na przedziale [min,max] oraz dla zadanej liczby losowań n. Ponadto, funkcja powinna zwrócić przez referencję (ponieważ w języku C/C++ funkcja nie może zwrócić dwóch wartości) wydajność tej metody.
Funkcję s(y) dobieramy tak, by zawsze znajdowała się powyżej funkcji g(y) i można z niej było łatwo wygenerować liczbę pseudolosową (na przykład metodą transformacji rozkładu jednorodnego z wykorzystaniem odwrotności dystrybuanty; na wykładzie przykład z funkcją liniową).
Wszystkie obliczenia należy wykonać dla funkcji typu:
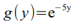
Uwagi
- Funkcja kwadratowa i jej odwrotność:
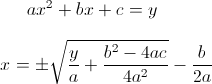
Wynik
Część pierwsza
Output:
Liczba Pi wynosi: 3.14392
Części druga i trzecia
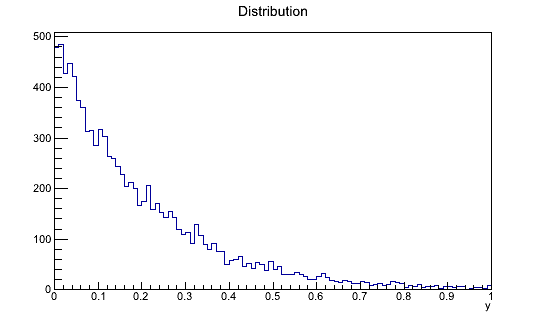
Output:
Calka: 0.199
Wydajnosc: 0.2072
Calka (metoda z funkcja pomocnicza): 0.198745
Wydajnosc (metoda z funkcja pomocnicza): 0.39749
Calka liczona metoda Integral: 0.198652