From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 27: |
Line 27: |
| | '''Uwaga 2!''' Jedynym parametrem, który nas interesuje to <code>double &f</code> - to jest minimalizowana wielkość. W naszym przypadku chcemy, by <code>f</code> było po prostu tożsame z chi-kwadrat. To oznacza, że '''wewnątrz''' funkcji <code>fcn</code> musimy wykonać iterację bin po binie z wczytanego pliku i dla każdego binu policzyć kwadrat różnic ( (model-wartosc_binu)^2/niepwnosc_binu^2 ). Ostateczna wartość <code>f</code>, zgodnie z definicją chi-kwadrat, to po prostu suma kwadratów różnic dla wszystkich binów. | | '''Uwaga 2!''' Jedynym parametrem, który nas interesuje to <code>double &f</code> - to jest minimalizowana wielkość. W naszym przypadku chcemy, by <code>f</code> było po prostu tożsame z chi-kwadrat. To oznacza, że '''wewnątrz''' funkcji <code>fcn</code> musimy wykonać iterację bin po binie z wczytanego pliku i dla każdego binu policzyć kwadrat różnic ( (model-wartosc_binu)^2/niepwnosc_binu^2 ). Ostateczna wartość <code>f</code>, zgodnie z definicją chi-kwadrat, to po prostu suma kwadratów różnic dla wszystkich binów. |
| | | | |
| - | 5. W funkcji głównej, mówimy naszemu obiektowi <code>gMinuit>, że ma skorzystać z funkcji FCN zdefiniowanej powyżej: | + | 5. W funkcji głównej, mówimy naszemu obiektowi <code>gMinuit</code>, że ma skorzystać z funkcji FCN zdefiniowanej powyżej: |
| | gMinuit->SetFCN(fcn); | | gMinuit->SetFCN(fcn); |
| | | | |
| Line 33: |
Line 33: |
| | gMinuit->DefineParameter(0, "p0", 100., 1., 0., 200.); | | gMinuit->DefineParameter(0, "p0", 100., 1., 0., 200.); |
| | | | |
| - | 7. Główna część zadania to wykonanie trzech komend: | + | 7. Główna część, gdzie dokonuje się zadania to wykonanie dwóch komend: |
| - | gMinuit->Command("MIGRAD"); | + | gMinuit->Command("MIGRAD"); |
| - | gMinuit->Command("MIGRAD");
| + | |
| | gMinuit->Command("MINOS"); | | gMinuit->Command("MINOS"); |
| | + | <code>MIGRAD</code> to algorytm szukający minimum funkcji <code>fcn</code> (czyli szuka najniższej wartości liczby <code>f</code>, którą definiujemy w określony przez nas sposób).<br> |
| | + | <code>MINOS</code> to algorytm używany po zminimalizowaniu <code>fcn</code>, który pozwala na dokładną estymację niepwności (w tym asymetrycznych).<br> |
| | + | '''Uwaga!''' Nie musimy znać szczegółów obu algorytmów. Dla zainteresowanych można poczytać [https://root.cern.ch/root/htmldoc/guides/minuit2/Minuit2Letter.pdf Minuit2Letter.pdf] |
| | | | |
| | == Wynik == | | == Wynik == |
Revision as of 09:15, 18 May 2020
Zadanie
Dopasowanie funkcji za pomocą paietu MINUIT (5 pkt.)
Chcemy wykonać dopasowanie do danych doświadczalnych (wczytywanych z pliku) nie używając funkci Fit, tylko za pomocą pakietu MINUIT (dokumentacja), który daje nam zdecydowanie większą kontrolę nad procesem dopasowania funkcji.
Kroki postępowania
1. Ściągamy plik z danymi: example_data.root i wczytujemy go w funkcji głównej makra.
2. Do naszych danych dopasujemy taką oto funkcję zdefiniowaną jako funkcja globalna (nasz model opisujący dane doświadczalne):
double model(double x, double *par)
{
double mu = par[3];
double sigma = par[4];
double norm = 1./sqrt(2.*TMath::Pi())/sigma;
double G = norm*exp(-0.5 *pow((x-mu)/sigma,2)); //unormowana funkcja Gaussa
double BinWidth = hist->GetBinWidth(1);
return par[0] + par[1]*x + par[2] * BinWidth * G;
}
3. W funkcji głównej makra tworzymy obiekt TMinuit, przykładowo:
TMinuit *gMinuit = new TMinuit(liczba_parametrow_fitu); //liczba parametrów wynika z definicji funkcji teoretycznej
4. Musimy stworzyć funkcję globalną (definiujemy ją przed funkcją główną), którą MINUIT będzie starał się zminimalizować manipulując naszymi parametrami. Musi ona mieć postać typu:
void fcn(int &npar, double *gin, double &f, double *par, int iflag)
Uwaga 1! Nie przerażamy się parametrami (to są automatyczne parametry, które muszą być i które potrzebuje MINUIT, my ich w ogóle nie użyjemy).
Uwaga 2! Jedynym parametrem, który nas interesuje to double &f - to jest minimalizowana wielkość. W naszym przypadku chcemy, by f było po prostu tożsame z chi-kwadrat. To oznacza, że wewnątrz funkcji fcn musimy wykonać iterację bin po binie z wczytanego pliku i dla każdego binu policzyć kwadrat różnic ( (model-wartosc_binu)^2/niepwnosc_binu^2 ). Ostateczna wartość f, zgodnie z definicją chi-kwadrat, to po prostu suma kwadratów różnic dla wszystkich binów.
5. W funkcji głównej, mówimy naszemu obiektowi gMinuit, że ma skorzystać z funkcji FCN zdefiniowanej powyżej:
gMinuit->SetFCN(fcn);
6. Następnie ustawiamy parametry funkcji, np.:
gMinuit->DefineParameter(0, "p0", 100., 1., 0., 200.);
7. Główna część, gdzie dokonuje się zadania to wykonanie dwóch komend:
gMinuit->Command("MIGRAD");
gMinuit->Command("MINOS");
MIGRAD to algorytm szukający minimum funkcji fcn (czyli szuka najniższej wartości liczby f, którą definiujemy w określony przez nas sposób).
MINOS to algorytm używany po zminimalizowaniu fcn, który pozwala na dokładną estymację niepwności (w tym asymetrycznych).
Uwaga! Nie musimy znać szczegółów obu algorytmów. Dla zainteresowanych można poczytać Minuit2Letter.pdf
Wynik
Przykłądowy histogram z dopasowaniem:
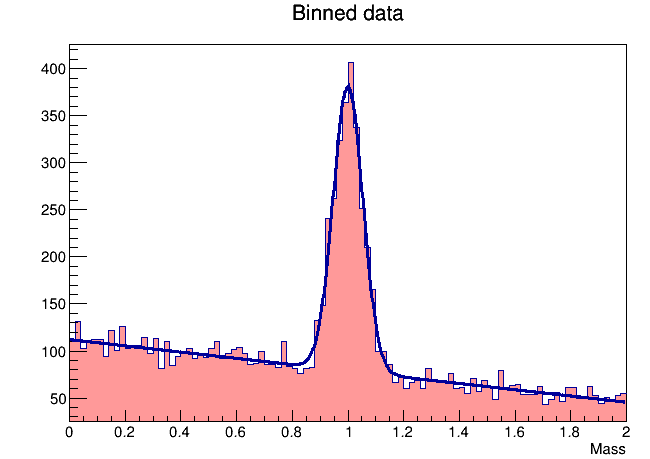
Ostateczny output:
FCN=93.6468 FROM MINOS STATUS=SUCCESSFUL 217 CALLS 364 TOTAL
EDM=3.79962e-17 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 0.0 per cent
EXT PARAMETER PARABOLIC MINOS ERRORS
NO. NAME VALUE ERROR NEGATIVE POSITIVE
1 p0 1.12163e+02 2.00576e+00 -2.00605e+00 2.00576e+00
2 p1 -3.33062e+01 1.52150e+00 -1.52151e+00 1.52153e+00
3 area 2.02070e+03 5.83151e+01 -5.82593e+01 5.83721e+01
4 mean 1.00031e+00 1.70385e-03 -1.70425e-03 1.70425e-03
5 width 5.34156e-02 1.50983e-03 -1.49782e-03 1.52309e-03
Info in <TCanvas::MakeDefCanvas>: created default TCanvas with name c1
