From Łukasz Graczykowski
(Difference between revisions)
|
|
| (5 intermediate revisions not shown) |
| Line 1: |
Line 1: |
| - |
| |
| | == Zadanie == | | == Zadanie == |
| | ''Część pierwsza'': '''Rozkład chi-kwadrat''' (3 pkt.) | | ''Część pierwsza'': '''Rozkład chi-kwadrat''' (3 pkt.) |
| Line 7: |
Line 6: |
| | ''Część druga'': '''Dopasowanie funkcji Gaussa''' (2 pkt.) | | ''Część druga'': '''Dopasowanie funkcji Gaussa''' (2 pkt.) |
| | | | |
| - | Napisać skrypt dokonujący splotu n rozkładów jednostajnych. Liczbę n należy wyznaczyć jako najmniejszą liczbę dodanych rozkładów, dla której wartość chi2/ndf, obliczona na podstawie dopasowania funkcji Gaussa (wykorzystując gotowe funkcje klasy TF1 - używamy funkcji Fit) jest mniejsza od 1.0. | + | Napisać skrypt dokonujący splotu n rozkładów jednostajnych. Liczbę n należy wyznaczyć jako najmniejszą liczbę dodanych rozkładów, dla której wartość chi2/ndf, obliczona na podstawie dopasowania funkcji Gaussa (wykorzystując gotowe funkcje klasy TF1 - używamy funkcji <code>Fit</code>) jest mniejsza od 1.0. |
| | + | |
| | + | == Uwagi == |
| | + | * Przechodzimy do '''drugiej części''' naszego przedmiotu - do tej pory zajmowaliśmy się własnościami rozkładów prawdopodobieństwa, teraz będziemy się zajmować szukaniem parametrów rozkładów prawdopodobieństwa (czyli '''estymacją''') na podstawie skończonej próby losowej (np. przeprowadzonego eksperymentu) |
| | + | * Czytamy dokładnie '''Wykład 8''' [http://www.if.pw.edu.pl/~lgraczyk/KADD2019/Wyklad8-2019.pdf link] - zwłaszcza slajdy dotyczące pobierania próby losowej z rozkładu normalnego (22-27) - najlepiej jednak przeczytać cały wykład, łącznie z wyjaśnieniem czym są estymatory i dlaczego rozkład chi-kwadrat jest taki ważny |
| | + | * W części pierwszej do rozkładu chi-kwadrat należy zaimplementować wzór ze slajdu 24 - współczynnik '''k''' zawiera fumkcję gamma (<code>TMath::Gamma</code>) |
| | + | * W części drugiej wykonujemy n rozkładów jednorodnych i wynikowy histogram dopasowujemy funkcją Gaussa - powinna to być pętla (np. <code>while</code> albo <code>do-while</code>), którą przerywamy w momencie, gdy wartość statystyki testowej chi-kwadrat (X^2) dzielona na liczbę stopni swobody (NDF) jest mniejsza od 1. Do obliczania X^2 oraz NDF są odpowiednie funkcje w klasie TF1 (nie robimy tego ręcznie) |
| | | | |
| | == Wynik == | | == Wynik == |
Latest revision as of 08:48, 27 April 2020
Zadanie
Część pierwsza: Rozkład chi-kwadrat (3 pkt.)
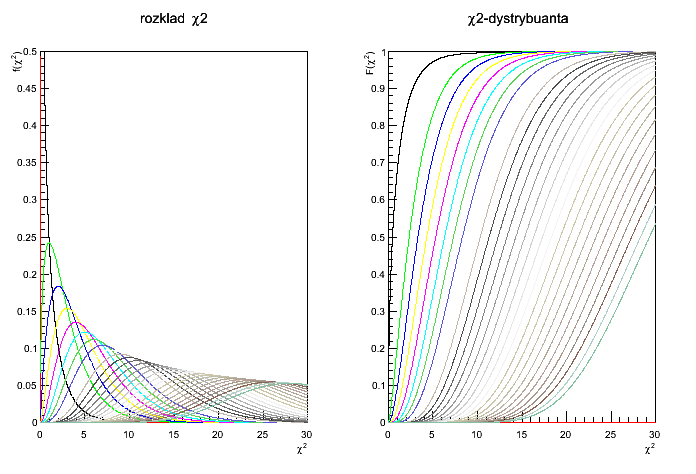
Napisać skrypt rysujący wykres rozkładu chi-kwadrat oraz jego dystrybuanty dla różnych wartości liczby stopni swobody: n=1..20.
Część druga: Dopasowanie funkcji Gaussa (2 pkt.)
Napisać skrypt dokonujący splotu n rozkładów jednostajnych. Liczbę n należy wyznaczyć jako najmniejszą liczbę dodanych rozkładów, dla której wartość chi2/ndf, obliczona na podstawie dopasowania funkcji Gaussa (wykorzystując gotowe funkcje klasy TF1 - używamy funkcji Fit) jest mniejsza od 1.0.
Uwagi
- Przechodzimy do drugiej części naszego przedmiotu - do tej pory zajmowaliśmy się własnościami rozkładów prawdopodobieństwa, teraz będziemy się zajmować szukaniem parametrów rozkładów prawdopodobieństwa (czyli estymacją) na podstawie skończonej próby losowej (np. przeprowadzonego eksperymentu)
- Czytamy dokładnie Wykład 8 link - zwłaszcza slajdy dotyczące pobierania próby losowej z rozkładu normalnego (22-27) - najlepiej jednak przeczytać cały wykład, łącznie z wyjaśnieniem czym są estymatory i dlaczego rozkład chi-kwadrat jest taki ważny
- W części pierwszej do rozkładu chi-kwadrat należy zaimplementować wzór ze slajdu 24 - współczynnik k zawiera fumkcję gamma (
TMath::Gamma)
- W części drugiej wykonujemy n rozkładów jednorodnych i wynikowy histogram dopasowujemy funkcją Gaussa - powinna to być pętla (np.
while albo do-while), którą przerywamy w momencie, gdy wartość statystyki testowej chi-kwadrat (X^2) dzielona na liczbę stopni swobody (NDF) jest mniejsza od 1. Do obliczania X^2 oraz NDF są odpowiednie funkcje w klasie TF1 (nie robimy tego ręcznie)
Wynik
Rozkład chi-kwadrat
Dopasowanie funkcji Gaussa
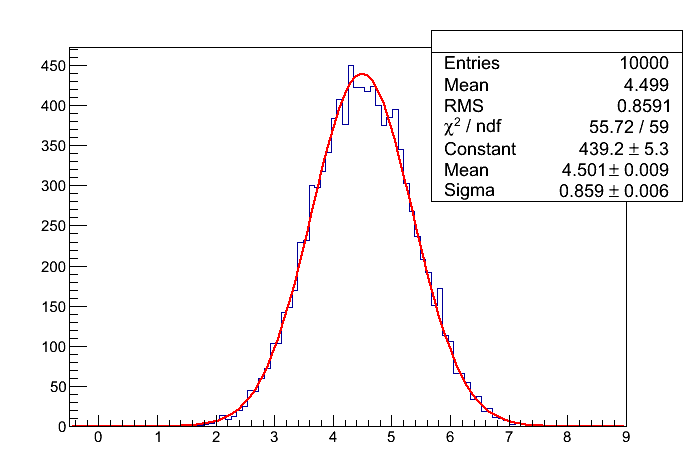
Output (przykładowy):
liczba splecionych rozkladow jednostajnych = 9
chi2/ndf = 55.724/59 = 0.944475

