From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 5: |
Line 5: |
| | == Zadanie == | | == Zadanie == |
| | Dana jest gęstość prawdopodobieństwa: | | Dana jest gęstość prawdopodobieństwa: |
| - | | + | [[File:funkcja_lab04_2012.png]] |
| - | <!--<math>f(x,y)=c\,e^{-(x^{2}+4y^{2}-2xy)}</math> -->
| + | |
| - | | + | |
| - | | + | |
| - | <math>f(x,y)=\left\lbrace \begin{array}{ll} c\,\cos(\frac{1}{2}x)\sin(y),&0\leqslant x\leqslant \pi \,\wedge\, 0\leqslant y\leqslant \pi\\0,&\text{pozostale przypadki}\end{array}\right. </math>
| + | |
| | | | |
| | Należy: | | Należy: |
Revision as of 08:57, 12 March 2012
Zadanie
Dana jest gęstość prawdopodobieństwa:
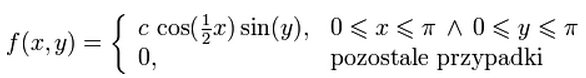
Należy:
- wyznaczyć stałą c w taki sposób aby rozkład gęstości był unormowany
- narysować histogram gęstości prawdopodobieństwa f(x,y) (1pkt)
- wyznaczyć i narysować histogram dystrybuanty F(x,y) (1pkt)
- wyznaczyć i narysować histogram gęstości brzegowej g(x) i h(y) (1pkt)
- wyznaczyć:
- wartości oczekiwane: E(X), E(Y) (0.5pkt)
- odchylenia standardowe sigma(X), sigma(Y) (0.5pkt)
- kowariancję cov(X,Y) (0.5pkt)
- współczynnik korelacji rho(X,Y) (0.5pkt)
Uwagi
- Do pracy z histogramami należy wykorzystać obiekty
TH1D i TH2D. Krótki przegląd możliwości tych obiektów można znaleźć w dokumencie: Histograms
Przykładowy wynik
Wykresy:
File:Lab04 2012.png
Output:
Wspolczynnik normujacy c=2.2687
E(X)=0.490066
E(Y)=0.655521
sigma(X)=0.287915
sigma(Y)=0.237391
cov(X,Y)=-0.000117787
rho(X,Y)=-0.00172334