Laboratorium SED - laboratorium 8

Z uczeniem bez nadzoru mamy do czynienia wtedy, gdy oryginalne dane nie posiadają przypisania do konkretnych klas tak, jak jest to np. w przypadku drzew decyzyjnych. Nie następuje tu więc proces uczenia się klasyfikatora na podstawie konkretnych przypadków.

Jednym z szerokich tematów w uczeniu bez nadzoru jest grupowanie, również nazywane analizą skupień czy klasteryzacja (od ang. cluster analysis). Podstawową ideą tego podejścia jest zbieranie (grupowanie) elementów tak, aby utworzyć (dość) jednorodne klasy. W ramach dzisiejszych zajęć zajmiemy się dwiema metodami: k-średnich oraz hierarchiczną.

Metoda k-średnich (ang. k-means), została szerzej omówiona na Wykładzie 7. Jej założenia są następujące:

W praktyce algorytm metody k-średnich inicjalizuje środki $K$ skupień (gdzie $K$ jest narzucone z góry) i w kolejnych iteracjach przypisuje najbliższe punkty do tych skupień oraz wyznacza nowe skupienia itd. aż w układzie nie będzie zachodzić żadna zmiana.

Do wizualizacji metody k-średnich w pakiecie użyjemy funkcji kmeans() z biblioteki cluster:

# Generowanie
draw.data.gauss <- function(S1, S2, m1, m2, n1, n2) {

X1 <- mvrnorm(n1, m1, S1)
X2 <- mvrnorm(n2, m2, S2)

X1 <- data.frame(X1); colnames(X1) <- c("x", "y")
X2 <- data.frame(X2); colnames(X2) <- c("x", "y")

X1$class <- 1; X2$class <- 2

data <- rbind(X1, X2); data$class <- factor(data$class)

return(data)
}

# Rysowanie punktów
plot.data <- function(data) {

cols <- c("blue", "orange")

plot(data[,1:2], col = cols[data$class], cex = 3, pch = 19)
text(data[,1:2], labels = 1:nrow(data), cex = 1, col = "white", font = 2)

}

# Parametry danych z rozkładu Gaussa
S1 <- matrix(c(2, 0, 0, 2), 2, 2)
S2 <- matrix(c(2, 0, 0, 2), 2, 2)

m1 <- c(-1, -1)
m2 <- c(1, 1)

n1 <- 10
n2 <- 10

# Ustawienie ziarna dla losowania danych
set.seed(1290)

# Generowanie obserwacji
data <- draw.data.gauss(S1, S2, m1, m2, n1, n2)

# Definiowanie kolorów
blueop <- "#0000ff55"; orangeop <- "#ffa50055"; redop <- "#00ff0055"

# Algorytm k-średnich dla K=2
par(mfrow = c(1,2))
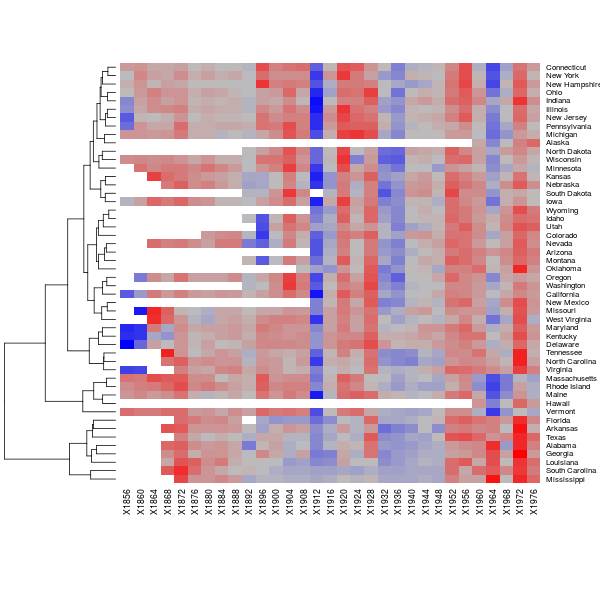
plot.data(data)
title("Oryginalne dane")

km2 <- kmeans(data[,1:2], 2)
plot.data(data)
title("Oryginalne dane + efekty k-średnich")
points(data[,1:2], pch = 19, cex = 4, col = c(blueop, orangeop)[km2$cluster])

Oczywiście liczba $K=2$ została przez nas z góry narzucona. Równie dobrze można zażądać wyszukiwania 3 skupień. Przy okazji możemy też zwizualizować fakt, że algorytm nie zawsze prowadzi do tych samych wyników.

# Algorytm k-średnich dla K=3
plot.clust <- function(n, data, K) {

km <- kmeans(data[,1:2], K)

plot(data[,1:2], pch = 19, cex = 3, col = c("blue", "orange", "green")[km$cluster])
text(data[,1:2], labels = 1:nrow(data), cex = 1, col = "white", font = 2)
title(n)
return(km$tot.withinss)
}

par(mfrow = c(3,3))
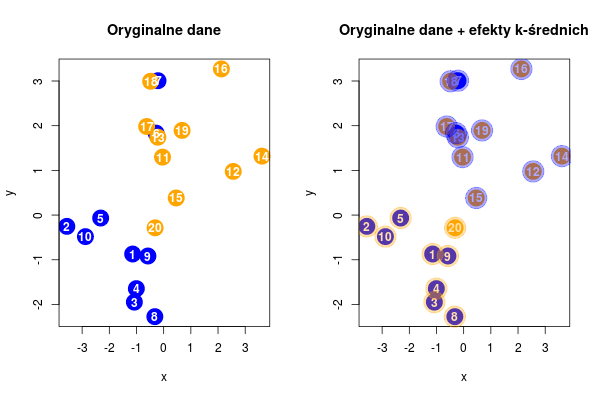
W <- sapply(1:9, function(n) plot.clust(n, data, 3))

Jak widać, w niektórych przypadkach mamy do czynienia jedynie ze zmianą numeracji klasy (czyli kolorów). Jednak są przypadki, dla których podział na klastry daje znacząco inne efekty. Aby wybrać optymalny podział korzystamy z pola $tot.withinss oddającego wartość $W$.

Patrząc na wyniki z poprzedniej części powstaje dość oczywiste pytanie: jaka wartość $K = K^*$ jest optymalna dla danego zbioru? Do wyznaczenia $K^{*}$ wykorzystamy tzw. statystykę odstępu (ang. gap statistics). Poniżej dane, z których będziemy korzystać - bardzo podobne do tych, z których korzystaliśmy poprzednio.

library(Hmisc)

# Macierz kowariancji
S <- matrix(c(1,0,0,1),2,2)
# Wartosci średnie dla poszczególnych skupień
m1 <- c(4, 4)
m2 <- c(1, 1)
m3 <- c(4,-1)

kolory <- c(rep("orange", 30), rep("blue", 30), rep("green", 30))

# Losowanie punktów do klastrów
clust1 <- mvrnorm(30, m1, S)
clust2 <- mvrnorm(30, m2, S)
clust3 <- mvrnorm(30, m3, S)

# Zebranie punktów razem
all_points <- rbind(clust1, clust2, clust3)

# Wyznaczenie wartości min i max dla współrzędnych
xrange <- range(all_points[,1])
yrange <- range(all_points[,2])

xmin = xrange[1]; xmax = xrange[2]
ymin = yrange[1]; ymax = yrange[2]

# Rysowanie danych par(mfrow = c(1,2))
plot(all_points, col=kolory, pch=19, cex=2, xlab="X", ylab="Y", xlim=c(xmin,xmax), ylim=c(ymin,ymax))
title("Klastry", cex.main=1.4, font=2)

# Wykonanie metody k-średnich dla k=3
cl <- kmeans(all_points, 3)

# Nadrukowanie na klastrach przynależnosci do klas
# otrzymanej z metody k-średnich
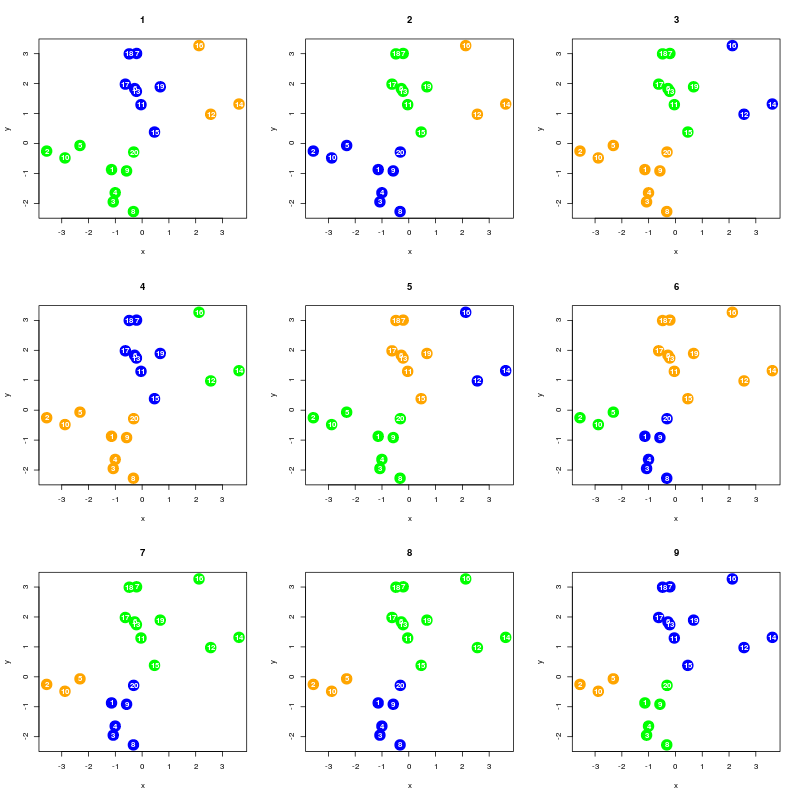
plot(all_points, col=kolory, pch=19, cex = 3, xlab="X", ylab="Y", xlim=c(xmin,xmax), ylim=c(ymin,ymax))
text(all_points[,1], all_points[,2], cl$cluster, col = "white", font=2) title("Metoda 3-średnich", cex.main=1.4, font = 2)

Punktem odniesienia w metodzie statystyki odstępu są dane losowe: w pudełku o wymiarach wyznaczonych przez skrajne współrzędne losujemy taką samą liczbę punktów co w danych oryginalnych lecz korzystamy z rozkładu jednorodnego.

# Dane losowe
rnd_points <- all_points

# Losowanie danych z rozkladu jednostajnego
rnd_points[,1] <- runif(90, xmin, xmax)
rnd_points[,2] <- runif(90, ymin, ymax)

# Rysowanie danych losowych
plot(rnd_points, pch=19, cex = 2, xlim=c(xmin,xmax), ylim=c(ymin,ymax), xlab="X", ylab="Y")
title("Dane losowe", cex.main=1.4, font=2)

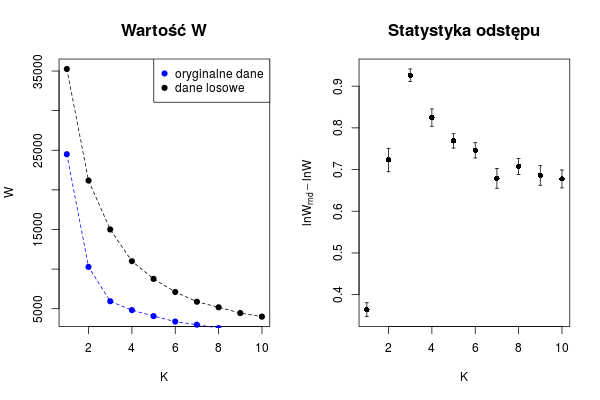
Wreszcie przechodzimy do kluczowego etapu procedury. Jak widać poniżej sama wartość $W$ jest niewystarczająca, gdyż po prostu spada wraz ze wzrostem $K$. W efekcie z dla każdej wartości $K$ liczmy $W$ z danych oryginalnych, a następnie tworzymy robimy to samo dla danych losowych (przy czym powtarzamy to $N$ razy) wyznaczając $\langle W_{rnd} \rangle = \sum_{i=1}^N W^i_{rnd}$. Staystyka odstępu dla danego $K$ jest zdefiniowana jako $\ln \langle W_{rnd} \rangle - \ln W$, a optymalną wartość $K = K^*$ bierze się z maksimum wykresu.

# Obliczanie statystyki odstepu
# Mamy od 1 do K skupien
# Dla kazdego skupienia przeprowadzamy N prob

K = 10
N = 20

# Deklaracja macierzy, w ktorych trzymamy wyniki
# z kolejnych interacji

dane <- array(0, dim = c(K, N))
dane_rnd <- array(0, dim = c(K, N))

# Główna pętla
for(c in 1:K) {
for(n in 1:N) {
cl <- kmeans(dist(all_points), c)

rnd_points[,1] <- runif(90, xrange[1], xrange[2])
rnd_points[,2] <- runif(90, yrange[1], yrange[2])

cl_rnd <- kmeans(dist(rnd_points), c)

dane[c,n] <- cl$tot.withinss
dane_rnd[c,n] <- cl_rnd$tot.withinss
}
}

# Wyznaczenie wartości średnich dla danych i danych losowych
# oraz odchyleń dla danych losowych

avgW <- apply(dane, 1, mean)
avgWrnd <- apply(dane_rnd, 1, mean)
sdWrnd <- apply(dane_rnd, 1, sd)

# Rysowanie statystki odstępu
par(mfrow = c(1,2))
plot(1:K, avgWrnd, pch = 19, t="o", lty = 2, ylab = "W", xlab = "K")
points(1:K, avgW, pch = 19, t="o", lty = 2, col = "blue")
title("Wartość W", cex.main=1.4, font=2)
legend("topright", c("oryginalne dane", "dane losowe"), col = c("blue", "black"), pch = 19)

errbar(1:K, log(avgWrnd/avgW), log(avgWrnd+sdWrnd/sqrt(20))-log(avgW), log(avgWrnd-sdWrnd/sqrt(20))-log(avgW), xlab="K", ylab=expression(lnW[rnd]-lnW)) title("Statystyka odstępu", cex.main=1.4, font=2)

Innym posobem wykonania analizy skupień jest wykorzystanie metod hierarchicznych. Ich ogólny opis można zawrzeć w następujących punktach:

# Parametry danych z rozkładu Gaussa
S1 <- matrix(c(2, 0, 0, 2), 2, 2)
S2 <- matrix(c(2, 0, 0, 2), 2, 2)

m1 <- c(-1, -1)
m2 <- c(1, 1)

n1 <- 10
n2 <- 10

# Ustawienie ziarna dla losowania danych
set.seed(1290)

# Generowanie obserwacji
data <- draw.data.gauss(S1, S2, m1, m2, n1, n2)

# Rysowanie danych
par(mfrow = c(1,2))
plot.data(data); title("Dane")

# Tworzenie dendrogramu
hc <- hclust(dist(data[,1:2]))

# Rysowanie dendrogramu
plot(hc, hang = -1, ylab = "Odległość", xlab = "Numer obserwacji", main = "Dendrogram", sub = NA, cex = 0.9, font = 2)
# Obwódka klastrów
rect.hclust(hc, 2, border = c("blue", "orange"))

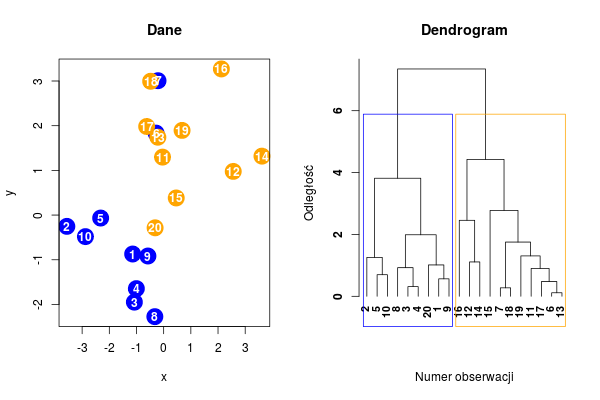
Kluczowe informacje dotyczące odległości, dla których tworzone są klastry oraz łączących się punktów są podane w polach $height oraz $merge (ujemne wartości oznaczają łączone obserwacje, natomiast dodatnie oddają klastry połączone w podanym kroku algorytmu - np. -17 1, to połączenie obserwacji nr 17 z klastrem powstałym w pierwszym kroku).

# Wektor połączeń
print(hc$height)

[1] 0.1134074 0.2723499 0.3113741 0.4765396 0.5633944 0.6974915 0.9001276 0.9251001 1.0134697 1.1104037 1.2576203 1.3054874
[13] 1.7526470 1.9880677 2.4569027 2.7758910 3.8164530 4.4257007 7.3490213

# Dodanie linii na wysokości pierwszego połączenia
abline(h = hc$height[1], col = "red", lty = 2)

# Połączenia
print(hc$merge)

      [,1] [,2]
 [1,]   -6  -13
 [2,]   -7  -18
 [3,]   -3   -4
 [4,]  -17    1
 [5,]   -1   -9
 [6,]   -5  -10
 [7,]  -11    4
 [8,]   -8    3
 [9,]  -20    5
[10,]  -12  -14
[11,]   -2    6
[12,]  -19    7
[13,]    2   12
[14,]    8    9
[15,]  -16   10
[16,]  -15   13
[17,]   11   14
[18,]   15   16
[19,]   17   18

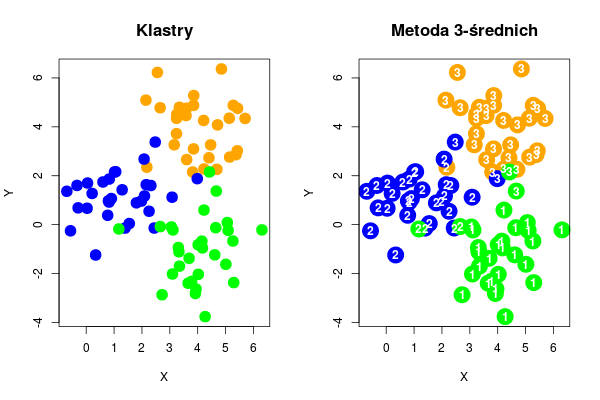
Bardzo spektakularnym sposobem wizualizacji danych jest funkcja heatmap. Umożliwia ona nie tylko prezentację samych trójwymiarowych danych ale także automatyczne stworzenie dendrogramów (opcja Colv=NA zapobiega tworzeniu dendrogramu dla kolumn). Jakbo zbiór danych posłuży nam zestawienie głosów oddanych na kandydatów Republikanów w wyobrach prezydenckich USA dla różnych lat i różnych stanów.