Statystyczna Eksploracja Danych
LABORATORIUM 6
DRZEWA: ALGORYTM KOSZTU-ZŁOŻONOŚCI
Jak już zostało wspomniane wcześniej, kwestia rozrostu drzewa nie jest jednoznaczna. Drzewo, w którego liściach znajdują się elementy tylko jednej klasy jest na pewno świetnym predyktorem dla zbioru treningowego, ale jego zdolności klasyfikacji załamują się dla nowych danych. Z drugiej strony, zbyt krótkie (tj. mało rozbudowane) drzewo też na pewno nie będzie doskonałe. Takie rozważania w jawny sposób prowadzą do problemu optymalizacyjnego, gdzie wybieramy pomiędzy zdolnością klasyfikującą drzewa a jego rozmiarem. Temat ten został poruszony na Wykładzie 4, w tym miejscu przypomnimy jedynie poniższą postać algorytmu kosztu-złożoności
gdzie \(\mathcal{T}\) oznacza dane drzewo, \(\hat{p}\) - frakcję błędnych klasyfikacji na drzewie \( \mathcal{T} \), \(N_{L}\) to liczba liści w tym drzewie, a \(\alpha\) (oznaczane też bardzo często jako \( cp \)) jets współczynnikiem złożoności.
Rzecz jasna, podstawiając \(\mathcal{T} = \mathcal{T}_0 \), czyli pełne drzewo oraz \(\alpha = 0\) otrzymujemy \(R_{cp} = 0\), natomiast wraz ze wzrostem \(\alpha\) drzewo \( \mathcal{T}_0\) przestaje być optymalne. Dla pewnej wartości \(\alpha \) otrzymujemy faktycznie optymalne drzewo, bilansujące składniki związane z liczbą błędnych klasyfikacji oraz rozmiarem.
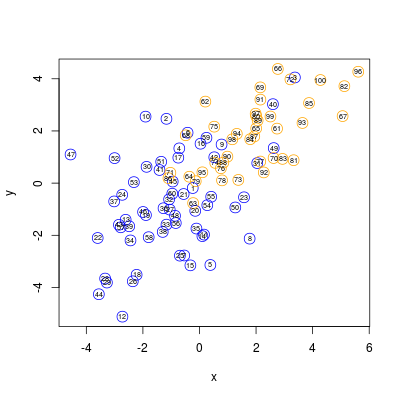
Zaczynamy w typowy sposób :-)
i wybieramy następujące parametry
Następnie tworzymy drzewo klasyfikujące podając parametry minsplit = 1, minbucket = 1, a także explicite cp = 0.
W tym momencie warto wypisać za pomocą funkcji printcp() najważniejszą dla dziesiejszych zajeć tabelę:
Classification tree:
rpart(formula = class ~ ., data = data, minsplit = 1, minbucket = 1,
cp = 0)
Variables actually used in tree construction:
[1] x y
Root node error: 40/100 = 0.4
n= 100
CP nsplit rel error xerror xstd
1 0.5250 0 1.000 1.000 0.122474
2 0.1750 1 0.475 0.650 0.109659
3 0.0500 2 0.300 0.525 0.101827
4 0.0125 5 0.150 0.450 0.096047
5 0.0000 16 0.000 0.525 0.101827
W tabeli zawarte są informacje dotyczące wartości parametru \(cp\) (czyli \(\alpha\)), rozmiaru drzewa (a dokładniej liczby podziałów), względnego błędu powtórnego postawienia, względnego błędu w przypadku kroswalidacji, a także odchylenie standardowego dla tego ostatniego przypadku. Warto przy tym zwrócić uwagę, że ze względu na losowy charakter kroswalidacji, powtórne wywołanie funkcji rpart() i funkcji printcp() zwykle daje inne wyniki dla dwóch ostatnich kolumn.
Classification tree:
rpart(formula = class ~ ., data = data, minsplit = 1, minbucket = 1,
cp = 0)
Variables actually used in tree construction:
[1] x y
Root node error: 40/100 = 0.4
n= 100
CP nsplit rel error xerror xstd
1 0.5250 0 1.000 1.000 0.122474
2 0.1750 1 0.475 0.625 0.108253
3 0.0500 2 0.300 0.575 0.105208
4 0.0125 5 0.150 0.425 0.093908
5 0.0000 16 0.000 0.575 0.105208
Oczywiście powstaje pytanie, dalaczego widzimy takie, a nie inne wartości parametru \(cp\)? Po prostu są to wartości progowe, dla których następuje zmiana budowy drzewa - pomiędzy kolejnymi progami statystyki pozostają takie same. Za "reprezentatywne" punkty uznaje się średnie kolejnycb progów, a dokładniej - średnie ważone, tj. \(\beta_i = \sqrt{\alpha_{i-1}\alpha_i}\). Widać to dobrze po wywołaniu komendy plotcp()
Za pomocą tego rysunku można dokonać wyboru optymalnego parametru \(cp\). W tym wypadku wybór teoretycznie powinien paść na wartość \(cp = 0.025 \), czyli znajdujący się pomiedzy \(cp = 0.0125 \) i \(cp = 0.05 \). Często jednak po początkowym spadku wartości \(R_{\alpha}\) następuje wypłaszczenie (plateau), tzn kolejne wartości \(R_{\alpha}\) niewiele się od siebie różnią. Jednakże wraz ze spadkiem \(\alpha\) zwiększa się rozmiar drzewa. Aby obejść ten problem, stosuje się regułę 1-SE, czyli jednego odchylenia standardowego. Oznacza to, że wybieramy taki punkt o mniejszym \(\alpha\), który mieści się w przedziale minimum powiększonego o jego odchylenie - na rysunku ta wartośc jest zaznaczona kreskowaną linią. W efekcie, dla rozpatrywanego przypadku bierzemy \(cp = 0.094\) i dla niego dokonujemy przycięcia (prune()) drzewa
DRZEWA: LICZBA KLAS \(G > 2 \)
Warto tu krótko wspomnieć, że nie ma żadnych powodów, dla których nie można wykonywać analizy klasyfikacji za pomocą drzew w przypadku więcej niż dwóch klas. Za przykład niech posłuży znany zbiór danych dotyczący irysów, zaimplementowany domyślnie w