Statystyczna Eksploracja Danych
LABORATORIUM 5
DRZEWA: PODZIAŁ NA ARGUMENTACH
Dzisiejsze zajęcia dotyczą drzew klasyfikujących, omówionych podczas Wykładu 4
Najistotniejszym elemntem konstrukcji drzew jest reguła podziału, która decyduje o tym, w jaki sposób poszczególne elementy skupione w danym węźle zostaną przesunięte do swoich węzłów-dzieci. Ze względu na swoja prostotę obliczeniową będziemy korzystać z miary różnorodności danej wskaźnikiem Gini'ego. Przedstawia się ona w następujący sposób, przy czym \(p\) ułamkiem obserwacji należących do klasy 1
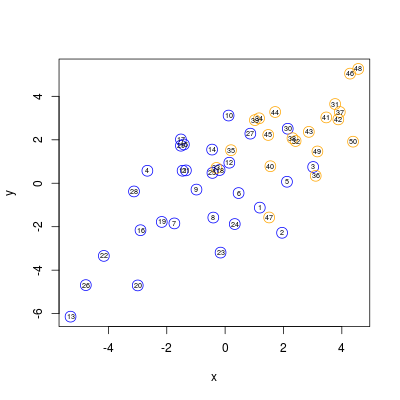
Rozpoczynamy od wylosowania danych z rozkładów Gaussa
przedstawiających się w następujący sposób
Teraz należy stworzyć cały "silnik" drzewa, czyli zdefiniowac współczynnik Gini'ego oraz funkcję do wyznaczania różnorodności, a dokładniej różnicy różnorodności pomiędzy rodzicem a dziećmi.
W tym momencie nie przedstawia już trudności wyznaczenie różnicy różnorodności dla każdej wartości podziału zarówno argumentu \(x\) jak i \(y\) danych.
Wartości te można wykreślić i porównać ze sobą.
Jak widać z wykresu, maksymalna wartość dla argumentu \(x\) jest większa niż dla \(y\), tak więc ona zostanie wybrana jako dzieląca zbiór danych, przy czym biorąc pod uwagę iż de facto mówimy o całym przedziale, wygodnie jest przyjąć wartość średnią z dwóch sąsiednich punktów
Można wreszcie zaznaczyć ostateczny podział na oryginalnym wykresie danych.
DRZEWA: PODZIAŁ DANYCH
Korzystając z powyższych funkcji gini(), norm.tab() oraz get.Q(), możemy teraz zaproponować bardzo prostą funkcję dostosowaną do przypadku dwóch argumentów, która wyszuka najlepszy podział na argumentach oraz korzystając z tego rozdzieli dane.
Daje to np. możliwość wizualizacji następnego podziału
oraz kolejnych
Warto przy tym zauważyć, że podziały w rogach prawym górnym oraz lewym górnym są ostateczne: w prostokątach pozostały jedynie elementy jednej klasy.
DRZEWA: PEŁNA FUNKCJA
Powyższe rozważania dają nam możliwość wykonania prymitywnej funkcji do implementacji drzewa klasyfikującego w przypadku dwóch argumentów. Funkcja działa rekurencyjnie i ma na celu dopowoadzenie do takiej sytuacji, aby w liściach znajdowały się jedynie elementy jednej klasy
dającej poniższy efekt
Podzial na X 0.9428313
Podzial na Y 0.6573468
Lisc drzewa, klasa A: 18 klasa B: 0
Podzial na Y 1.535119
Podzial na Y 1.233252
Podzial na Y 0.8255293
Lisc drzewa, klasa A: 0 klasa B: 1
Lisc drzewa, klasa A: 1 klasa B: 0
Lisc drzewa, klasa A: 0 klasa B: 1
Lisc drzewa, klasa A: 6 klasa B: 0
Podzial na Y 0.765695
Podzial na X 3.061114
Podzial na Y -1.348321
Podzial na Y -1.927858
Lisc drzewa, klasa A: 1 klasa B: 0
Lisc drzewa, klasa A: 0 klasa B: 1
Lisc drzewa, klasa A: 3 klasa B: 0
Lisc drzewa, klasa A: 0 klasa B: 1
Podzial na X 2.227567
Podzial na X 1.930539
Lisc drzewa, klasa A: 0 klasa B: 5
Lisc drzewa, klasa A: 1 klasa B: 0
Lisc drzewa, klasa A: 0 klasa B: 11
PAKIET RPART
Oczywiście, celem powyższych rozważań i bardzo prostych funkcji jest jedynie ilustracja problemu. Do wykorzystywania drzew klasyfikujących w pakiecie R jest dedykowana biblioteka rpart, której główną funkcją jest imienniczka pakietu rpart(). Poniżej wywołamy ją z argumentami minsplit=1 oraz minbucket=1. Pierwszy z parametrów określa minimalną liczbę elementów, które muszą się znaleźć w weźle, aby dochodziło do podziału. Drugi - minimalną liczbę obserwacji, która musi znaleźć się w węźle, aby został uznany za liść. Wybrane przez nas parametry są bardzo "agresywne", czyli de facto będą raczej prowadzić do przetrenowania drzewa, ale pozwolą nam porównać nowe wyniki z poprzednio otrzymanymi.
n= 50
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 50 20 1 (0.60000000 0.40000000)
2) x< 0.9428313 27 2 1 (0.92592593 0.07407407)
4) y< 0.6573468 18 0 1 (1.00000000 0.00000000) *
5) y>=0.6573468 9 2 1 (0.77777778 0.22222222)
10) y>=1.535119 6 0 1 (1.00000000 0.00000000) *
11) y< 1.535119 3 1 2 (0.33333333 0.66666667)
22) y>=0.8255293 2 1 1 (0.50000000 0.50000000)
44) y< 1.233252 1 0 1 (1.00000000 0.00000000) *
45) y>=1.233252 1 0 2 (0.00000000 1.00000000) *
23) y< 0.8255293 1 0 2 (0.00000000 1.00000000) *
3) x>=0.9428313 23 5 2 (0.21739130 0.78260870)
6) y< 0.765695 6 2 1 (0.66666667 0.33333333)
12) x< 3.061114 5 1 1 (0.80000000 0.20000000)
24) y>=-1.348321 3 0 1 (1.00000000 0.00000000) *
25) y< -1.348321 2 1 1 (0.50000000 0.50000000)
50) y< -1.927858 1 0 1 (1.00000000 0.00000000) *
51) y>=-1.927858 1 0 2 (0.00000000 1.00000000) *
13) x>=3.061114 1 0 2 (0.00000000 1.00000000) *
7) y>=0.765695 17 1 2 (0.05882353 0.94117647)
14) x< 2.227567 6 1 2 (0.16666667 0.83333333)
28) x>=1.930539 1 0 1 (1.00000000 0.00000000) *
29) x< 1.930539 5 0 2 (0.00000000 1.00000000) *
15) x>=2.227567 11 0 2 (0.00000000 1.00000000) *
Bibioteka rpart umożliwia także stworzenie graficznej reprezentacji drzewa za pomocą przeciążonej funkcji plot, do której należy dodać odpowiednie opcje związane z tekstem.
Trzeba jednak uczciwie przyznać, że podstawowy rysunek jest, delikatnie mówiąc, daleki od doskonałości. Z pomocą przychodzi biblioteka rpart.plot z dedykowaną funkcją rpart.plot(), umożliwiającą otrzymanie duuużo lepszego efektu...
DRZEWA: PRZEWIDYWANIE
Rzecz jasna, drzewa służą do przewidywania, tzn klasyfikacji nowych danych. Jeśli wykorzystamy nasze drzewo do powtórnej klasyfikacji, otrzymamy pełną zgodność.
Jednak taki klasyfikator jest niewątpliwie "przeuczony". Wywołamy teraz funkcję rpart() dla domyślnych parametrów
i dokonamy przewidywania za jej pomocą
Jak widać, efekty nie są dużo gorsze. Sytuacja może się jeszcze bardziej zmienić w przypadku wykorzystania nowych danych.