Statystyczna Eksploracja Danych
LABORATORIUM 4
METODA K-NN
Zgodnie z teorią metoda k najbliższych sąsiadów (k nearest neighbors) jest dość prostym sposobem na bezpośrednie określenia przynależności danych obserwacji do poszczególnych klas. Wykorzystuje następującą regułę: do danego punktu w przestrzeni przypisz taką klasę, jaką ma większość jego \(k_{nn}\) sąsiadów, przy czym liczba \(k_{nn}\) jest z góry narzucona. Rozpatrzmy na początek prosty przypadek dwóch klas; zacznijmy od wygenerowania danych.
library(MASS)
draw.data.gauss <- function(S1, S2, m1, m2, n1, n2) {
X1 <- mvrnorm(n1, m1, S1)
X2 <- mvrnorm(n2, m2, S2)
X1 <- data.frame(X1); colnames(X1) <- c("x", "y")
X2 <- data.frame(X2); colnames(X2) <- c("x", "y")
X1$class <- 1; X2$class <- 2
data <- rbind(X1, X2); data$class <- factor(data$class)
return(data)
}
# Parametry danych z rozkladu Gaussa
S1 <- matrix(c(4, 2, 2, 4), 2, 2)
S2 <- matrix(c(4, 2, 2, 2), 2, 2)
m1 <- c(-1, -1)
m2 <- c(2, 2)
n1 <- 30
n2 <- 20
# Generowanie obserwacji
data <- draw.data.gauss(S1, S2, m1, m2, n1, n2)
Nasza procedura nie będzie optymalna - wykorzystamy w niej macierz \(\mathbf{M}\) odegłości pomiędzy wszystkimi obserwacjami, którą otrzymamy dzięki funkcji dist(). Dla danej obserwacji będziemy:
- brać jeden rząd (lub kolumnę) macierzy \(\mathbf{M}\) odpowiadający wektorowi odległości od danego punktu,
- sortować wektor rosnąco według odległości,
- pobierać indeksy (numery) pierwszych \(k_{nn}\) obserwacji w tym posortowanym wektorze,
- obliczać klasę większościową tak wybranych punktów.
Te skomplikowane w opisie czynności realizuje kod poniżej
# Prosta funkcja do wyznaczania przynależnosci
# metoda k-nn
find.knn <- function(class, M, k) {
k.nodes <- order(M)[1:k]
tab <- table(class[k.nodes])
return(rownames(tab)[which.max(tab)])
}
# Macierz odległości
M <- as.matrix(dist(data[,1:2]))
# Klasyfikacja za pomocą prostej funkcji
class.own <- sapply(1:nrow(data), function(i) find.knn(data$class, M[i,], 1))
W tym momencie należy przetestować powyższe wyniki z generyczną funkcją knn() z biblioteki class. Ma ona trochę dziwaczną postać, gdyż od razu podajemy zarówno zbiór treningowy jak i testowy. Parametrem jest także liczba najbliższych sąsiadów. Poniżej wykorzystamy także funkcję table(), aby ostatecznie porównać wyniki.
library(class)
# Funkcja knn
class.knn <- knn(data[,1:2], data[,1:2], data$class, 1)
# Porównanie
table(class.knn, class.own)
Łatwiejszym sposobem porównania jest wykreślenie granicy klas dla siatki punktów. Przy okazji będziemy mogli nanieść dane na wykres i sprawdzić jakość wyników.
# Rysowanie punktów
plot.data <- function(data) {
cols <- c("blue", "orange")
plot(data[,1:2], col = cols[data$class], cex = 2)
text(data[,1:2], labels = 1:nrow(data), cex = 0.6)
}
# Rozpinanie siatki
xp <- seq(-10, 10, 0.1)
yp <- seq(-10, 10, 0.1)
gr <- expand.grid(x = xp, y = yp)
# Klasyfikacja na siatce za pomocą prostej funkcji
gr.k <- sapply(1:nrow(gr), function(i) find.knn(data$class, sqrt((data$x-gr$x[i])^2 + (data$y - gr$y[i])^2), 1))
# Klasyfikacja na siatce za pomocą funkcji knn
k1 <- knn(data[,1:2], gr, data$class, 1)
# Wykreślanie punktów
plot.data(data)
# Granica klasyfikacyjna za pomocą prostej funkcji
contour(xp, yp, matrix(gr.k == "1", length(xp)), add = T, levels = 0.5, lwd = 2, col = "blue")
# Granica za pomocą funkcji knn
contour(xp, yp, matrix(k1 == "1", length(xp)), add = T, levels = 0.5, col = "orange", lty = 2, lwd = 2)
Efektem jest poniższy rysunek
Rysunek 4.1
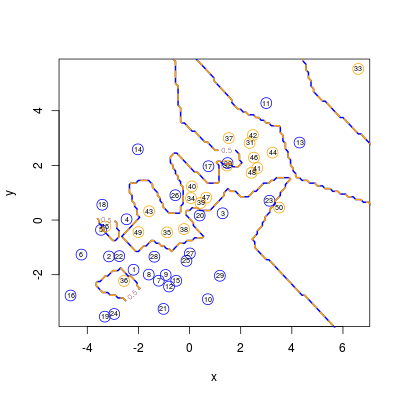
Dla przypadku \(k_{nn}=2\) otrzymujemy osobliwy kształt. Dlaczego?
Rysunek 4.2

METODA C-NN
Spora część obserwacji jest niepotrzebna do wykonania klasyfikacji z \(k_{nn}=1\). Aby zminimalizować zbiór punktów konieczny do poprawnej (lub prawie poprawnej) klasyfikacji można wykorzystac metodę c-nn (condensed nearest neighbors). Pakiet class realizuje tę operację za pomocą dwóch funkcji: najpierw wywołujemy funkcje condense(), a następnie korzystając z jej wyników - funkcję reduce.nn().
# Rysujemy punkty
plot.data(data)
# Uruchamiamy wstępną funkcję
nodes.cond <- condense(data[,1:2], data$class)
# Zaznaczamy punkty
points(data[nodes.cond,1:2], cex = 3, col = "red", pch = 22, lwd = 2)
Pierwsza funkcja daje efekt podobny do poniższego
Rysunek 4.3
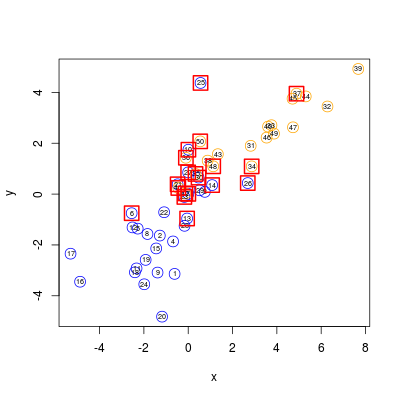
# Uruchamiamy drugą funkcję
nodes.red <- reduce.nn(data[,1:2], nodes.cond, data$class)
# Rysujemy punkty od nowa i zaznaczamy je
plot.data(data)
points(data[nodes.red,1:2], cex = 3, col = "red", pch = 22, lwd = 2)
natomiast druga - następujący:
Rysunek 4.4
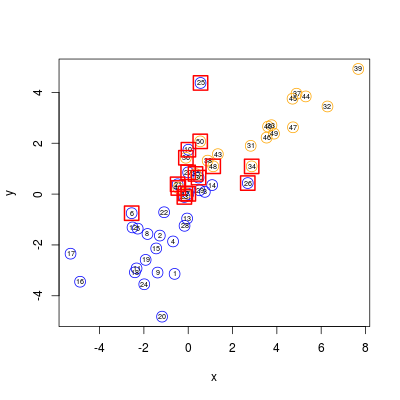
Dodatkowo możemy jeszcze przetestować skuteczność podejścia
# Testujemy skuteczność
table(data$class, knn(data[nodes.red,1:2], data[,1:2], data$class[nodes.red]))
METODA K-NN DLA WIELU KLAS
W przypadku więcej niż dwóch klas wygodnie będzie użyć funkcji image() do wykonania obszarów przynależności klas. Na początek zmodyfkujemy funkcję do losowania punktów.
draw.data.gauss3 <- function(S1, S2, S3, m1, m2, m3, n1, n2, n3) {
X1 <- mvrnorm(n1, m1, S1)
X2 <- mvrnorm(n2, m2, S2)
X3 <- mvrnorm(n3, m3, S3)
X1 <- data.frame(X1); colnames(X1) <- c("x", "y")
X2 <- data.frame(X2); colnames(X2) <- c("x", "y")
X3 <- data.frame(X3); colnames(X3) <- c("x", "y")
X1$class <- 1; X2$class <- 2; X3$class <- 3
data <- rbind(X1, X2, X3); data$class <- factor(data$class)
return(data)
}
Następnie losujemy obserwacje z rozkładów o zadanych parametrach
S1 <- matrix(c(4, 2, 2, 4), 2, 2)
S2 <- matrix(c(4, 2, 2, 2), 2, 2)
m1 <- c(-1, -1)
m2 <- c(2, 2)
m3 <- c(-2, 2)
n1 <- 30
n2 <- 20
n3 <- 30
data <- draw.data.gauss3(S1, S2, S2, m1, m2, m3, n1, n2, n3)
Mając już dane, wyznaczamy skrajne punkty dla współrzędnych i rozpinamy siatkę (50 na 50 elementów). Kolejnym krokiem jest uruchomienie funkcji knn() na danej siatce (dla \(k_{nn}=1\)) i wreszcie wykreślenie obszarów oraz dodanie punktów
xp <- with(data, seq(min(x), max(x), length = 50))
yp <- with(data, seq(min(y), max(y), length = 50))
gr <- expand.grid(x = xp, y = yp)
gr.knn <- knn(data[,1:2], gr, data$class, 1)
image(x = xp, y = yp, matrix(as.numeric(gr.knn), 50), xlab = "x", ylab = "y")
points(data[,1:2], col = data$class, pch = 19)
otrzymując np. taki efekt
Rysunek 4.5
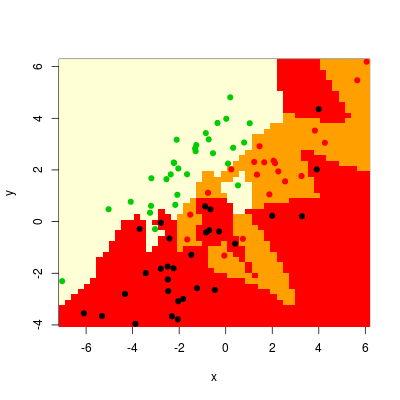
Jeszcze ciekawsze jest porównanie rysunków dla kilku wartości \(k_{nn}\). Realizuje to poniższy kod, gdzie zastosowano funkcję apr() modyfikującą cechy obrazu (tu: wprowadzenie siatki obrazków 2 x 2).
par(mfrow = c(2,2))
gr.knn <- knn(data[,1:2], gr, data$class, 1)
image(x = xp, y = yp, matrix(as.numeric(gr.knn), 50), xlab = "x", ylab = "y")
title("k=1")
points(data[,1:2], col = data$class, pch = 19)
gr.knn <- knn(data[,1:2], gr, data$class, 2)
image(x = xp, y = yp, matrix(as.numeric(gr.knn), 50), xlab = "x", ylab = "y")
title("k=2")
points(data[,1:2], col = data$class, pch = 19)
gr.knn <- knn(data[,1:2], gr, data$class, 3)
image(x = xp, y = yp, matrix(as.numeric(gr.knn), 50), xlab = "x", ylab = "y")
title("k=3")
points(data[,1:2], col = data$class, pch = 19)
gr.knn <- knn(data[,1:2], gr, data$class, 5)
image(x = xp, y = yp, matrix(as.numeric(gr.knn), 50), xlab = "x", ylab = "y")
title("k=5")
points(data[,1:2], col = data$class, pch = 19)
Rysunek 4.6
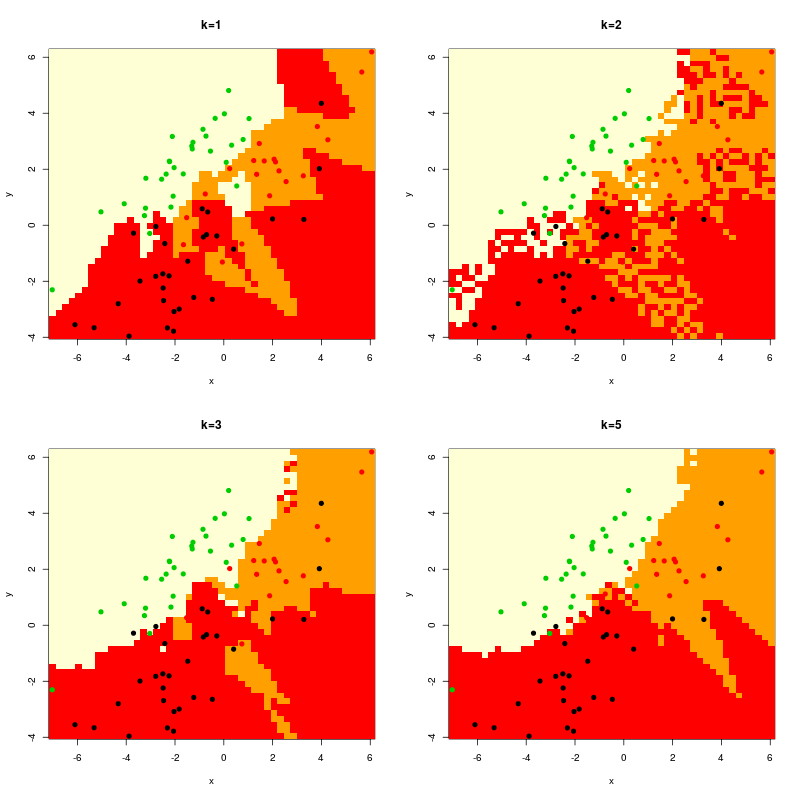
Zauważmy wygładzanie się obszarów dla coraz większych wartości \(k_{nn}\), jak również bardzo "poszarpaną" fakturę dla parzystej wartości \(k_{nn}\).
