Laboratorium SED - laboratorium 3

Na dzisiejszych zajęciach zajmiemy się przede wszystkim metodami oceny jakości klasyfikatorów. Zgodnie z Wykładem 3 podstawowym obiektem, który ułatwi nam pracę jest macierz pomyłek, oznaczana na potrzeby tych ćwiczeń jako $\mathbf{CM}$. Poszczególne pola tej macierzy

są określane jako TRUE NEGATIVE (dane: negatywne, predykcja: negatywna), FALSE POSITIVE (dane: negatywne, predykcja: pozytywna), FALSE NEGATIVE (dane: pozytywne, predyckja: pozytywna) oraz TRUE POSITIVE (dane: pozytywne, predykcja: pozytywna). Sumowanie rzędów $\mathbf{CM}$ daje informacje o oryginalnych klasach, sumowanie kolumn - o przewidywanych. Wygodnym wskaźnikiem jakości klasyfikatora jest jego dokładność (ACCURACY) zdefiniowana jako

innymi są FALSE POSITIVE RATE (FPR, 1 - specificity) oraz TRUE POSITIVE RATE (TPR, sensitivity)

Dla ustalenia uwagi znów zaczynamy od nieśmiertelnego rozkładu Gaussa w 2D. Tym razem zdefiniujemy funkcję draw.data.gauss(), którą będziemy wykorzystwać do losowania obserwacji z tego rozkładu (dodatkowo od razu ładujemy potrzebne biblioteki)

library(MASS)
library(klaR)
library(e1071)

draw.data.gauss <- function(S1, S2, m1, m2, n1, n2) {

X1 <- mvrnorm(n1, m1, S1)
X2 <- mvrnorm(n2, m2, S2)

X1 <- data.frame(X1); colnames(X1) <- c("x", "y")
X2 <- data.frame(X2); colnames(X2) <- c("x", "y")

X1$class <- 1; X2$class <- 2

data <- rbind(X1, X2); data$class <- factor(data$class)

return(data)
}

Następnie losujemy obserwacje z rozkładów o zadanych parametrach (liczności $n_1$, $n_2$, wektory średnich $\mathbf{m}_1$ i $\mathbf{m}_2$ oraz macierze kowariancji $\mathbf{S}_1$ i $\mathbf{S}_2$) i na takich danych, uważanych od tej chwili za PU (próba ucząca) budujemy klasyfikatory: LDA, QDA, a także naiwnego Bayesa

# Parametry danych z rozkladu Gaussa
S1 <- matrix(c(4, 2, 2, 4), 2, 2)
S2 <- matrix(c(4, 2, 2, 2), 2, 2)

m1 <- c(-1, -1)
m2 <- c(2, 2)

n1 <- 80
n2 <- 60

# Generowanie obserwacji
data <- draw.data.gauss(S1, S2, m1, m2, n1, n2)

# Trenowanie klasyfikatorów na PU
class.lda <- lda(class ~ x + y, data)
class.qda <- qda(class ~ x + y, data)
class.nb <- naiveBayes(class ~ x + y, data)

Teraz skonstruujemy funkcję CM.large(), której celem będzie wyznaczenie macierzy pomyłek, a następnie obliczenie istotnych, wyżej wymienionych cech, tzn. dokładności, TN, TP, FPR, TPR. Kolejnym krokiem będzie, znane już z poprzednich zajęć, dokonanie klasyfikacji za pomocą metody powtórnego podstawienia. Dodatkowo efekty działania funkcji CM.large() dla różnych klasyfikatorów umieścimy w jendej ramce danych tak, aby łatwo można było je porównać.

CM.large <- function(org.class, pred.class) {

CM <- table(org.class, pred.class)

# Skuteczność klasyfikatora
ACC <- sum(diag(CM)) / sum(CM)

# Wartości true positive i true negative
# zakładamy, że klasa "2" jest "pozytywna"
TP <- CM[2,2]
TN <- CM[1,1]

sums <- apply(CM, 1, sum)

TPR <- TP / sums[2]
FPR <- 1 - TN / sums[1]

return(c(ACC = round(ACC,4), TP = TP, TN = TN, TPR = round(TPR, 4), FPR = round(FPR, 4), row.names = NULL))
}

# Powtórne podstawienie
data.lda.old <- predict(class.lda, data)
data.qda.old <- predict(class.qda, data)
data.nb.old <- predict(class.nb, data)

# Główne wartości z macierzy pomyłek dla powtórnego podstawienia
res.old <- CM.large(data$class, data.lda.old$class)
res.old <- rbind(res.old, CM.large(data$class, data.qda.old$class))
res.old <- rbind(res.old, CM.large(data$class, data.nb.old))
rownames(res.old) <- c("LDA", "QDA", "NB")

       ACC TP TN  TPR.2  FPR.1
LDA 0.8643 52 69 0.8667 0.1375
QDA 0.8714 50 72 0.8333 0.1000
NB  0.8643 52 69 0.8667 0.1375

Powyższa tabela sugeruje, że wszystkie 3 testowane klasyfikatory miały podobne statystyki i ciężko mówić tu o jakimś "zwycięzcy". Trzeba zwrócić tu uwagę na fakt, że dokonywaliśmy powtórnego podstawienia, a więc otrzymane przez nas wartości można traktować jako dość "optymistyczne", gdyż klasyfikatory przewidywały przynależność do klas tych samych obserwacji, za pomocą których były trenowane. Należałoby więc powtórzyć te procedury dla zestawu innych danych (PW - próby walidacyjnej), co realizuje poniższy kod

# Generowanie obserwacji walidacyjnych
val <- draw.data.gauss(S1, S2, m1, m2, 30, 30)

# Predykcja na zbiorze walidacyjnym
data.lda.val <- predict(class.lda, val)
data.qda.val <- predict(class.qda, val)
data.nb.val <- predict(class.nb, val)
data.nb.val.p <- predict(class.nb, val, type = "raw")

res.val <- CM.large(val$class, data.lda.val$class)
res.val <- rbind(res.val, CM.large(val$class, data.qda.val$class))
res.val <- rbind(res.val, CM.large(val$class, data.nb.val))
rownames(res.val) <- c("LDA", "QDA", "NB")

       ACC TP TN  TPR.2  FPR.1
LDA 0.8167 23 26 0.7667 0.1333
QDA 0.8667 25 27 0.8333 0.1000
NB  0.8667 25 27 0.8333 0.1000

Jak widać, dla LDA w tym konkretnym przypadku jest kilkuprocentowy spadek, natomiast dla innych klasyfikatorów różnica jest minimalna.

Powyższe wartości (ACC, FPR, TPR) są punktowe, tzn. zakładają ustalony próg prawdopodobieństwa a posteriori, powodujący, że dana obserwacja zostaje przypisana do konkretnej klasy (dokładniej: próg równy 1/2). Czasem jednak istotne pytaniem staje się: jaki jest profil danego klasyfikatora, tzn. jak się zachowuje przy założeniu nierównego traktowania przynależności do klas. Taki profil często przedstawiany jest w postaci krzywej ROC (receiver-operating curve), gdzie na osi X zostają odłożone wartości FPR, natomiast na osi Y - TPR dla różnych poziomów odcięcia, czyli progów prawdopodobieństw a posteriori np. $p(2|\mathbf{x})$.

W celu otrzymania krzywej ROC musimy nieco zmodyfikować funkcję odpowiedzialną za wyznaczanie wartości FPR i TPR

CM.values <- function(org.class, pred.posterior, threshold) {
# Funkcja do wyznaczania wartości TPR (true positive rate) i FPR (false positive rate)
# jej argumenty to oryginalne klasy, wartosci prawdopodobienstw a posteriori dla klasyfikatora
# oraz wektor progow

# Korzystamy z prawdopodobieństw a posteriori
pred.class <- factor(ifelse(pred.posterior >= threshold, 2, 1))

# Wartości true positive i true negative
# zakładamy, że klasa "2" jest "pozytywna"
TP <- sum(pred.class == 2 & org.class == 2)
TN <- sum(pred.class == 1 & org.class == 1)

# Liczność oryginalnych klas
sum.neg <- sum(org.class == 1)
sum.pos <- sum(org.class == 2)

TPR <- TP / sum.pos
FPR <- 1 - TN / sum.neg

return(c(FPR,TPR))
}

Tworzymy też funkcję get.roc.values(), która realizuje następujące cele: pobiera wartości prawdopodobienstw a posteriori dla danej klasy, sortuje je i dla każdego z nich wywołuje funkcję CM.values(). W ten sposób do powyższej funkcji przekazywany jest wartość prawdopodobieństwa, która ma być traktowana jako próg $\tau$- obserwacje z $p(2|\mathbf{x})$ wyższą niż $\tau$ są klasyfikowane jako pochodzące z klasy "2".

get.roc.values <- function(class, posterior) {

progi <- c(-Inf, sort(unique(posterior)), +Inf)

z <- t(sapply(1:length(progi), function(i) CM.values(class, posterior, progi[i])))

return(z)
}

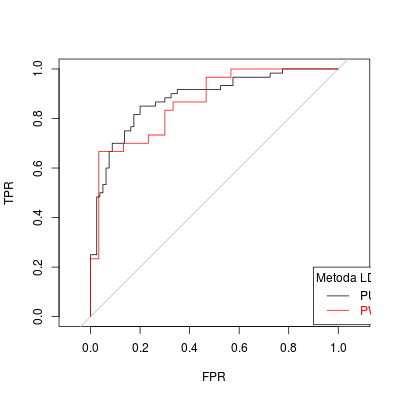
Możemy w końcu uruchomic liczenie ROC dla dówch przypadków LDA: PU oraz PW i porównać efekty na jedynm rysunku.

# Wartości FPR i TPR dla metody LDA
# w przypadku PU i PW
roc.lda.old <- get.roc.values(data$class, data.lda.old$posterior[,2])
roc.lda.val <- get.roc.values(val$class, data.lda.val$posterior[,2])

# Porównanie LDA
plot(roc.lda.old, t="l", xlab = "FPR", ylab = "TPR", asp = 1)
abline(0, 1, col = "gray")
lines(roc.lda.val, col = "red")
legend(0.9, 0.2, c("PU", "PW"), col = c("black", "red"), text.col = c("black", "red"), lty = 1, title = "Metoda LDA")

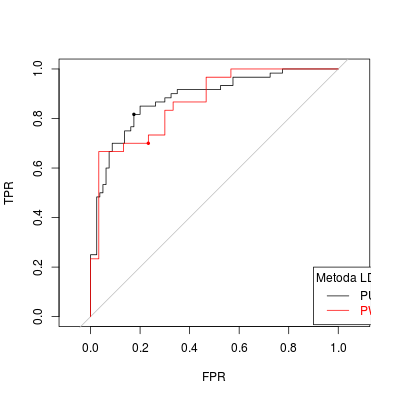
Oczywiście, możemy również odłożyć na krzywej ROC punkty, które odpowiadają konkretnym wartościom (np. tym, związanym z konkretnymi klasyfikatorami).

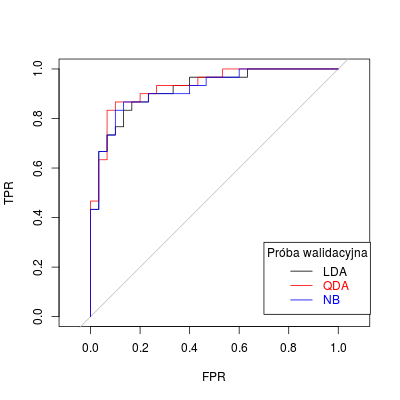
Wreszcie, a może przede wszystkim, krzywa ROC służy do porównywania różnych klasyfikatorów.

roc.lda.val <- get.roc.values(val$class, data.lda.val$posterior[,2])
roc.qda.val <- get.roc.values(val$class, data.qda.val$posterior[,2])
roc.nb.val <- get.roc.values(val$class, data.nb.val.p[,2])

plot(roc.lda.val, t="l", xlab = "FPR", ylab = "TPR", asp = 1)
abline(0, 1, col = "gray")
lines(roc.qda.val, col = "red")
lines(roc.nb.val, col = "blue")

legend(0.7, 0.3, c("LDA", "QDA", "NB"), col = c("black", "red", "blue"), text.col = c("black", "red", "blue"), lty = 1, title = "Próba walidacyjna")

W przypadku braku możliwości skorzystania z próby walidacyjnej (tzn. braku możliwości wydzielenia części danych) korzysta się z metody kroswalidacji (walidacji krzyżowej). W tym celu dzieli się dane na kilka (np. 5 lub 10) części, trenuje się klasyfikator na próbie powstałej przez usunięcie jednej części a testuje się na tej usuniętej. Procedurę powtarza się dla każdej częsci, zliczając pomyłki, a następnie sumując i dzieląc przez liczbę elementów, w ten sposób otrzymując oszacowanie błędu klasyfikatora.

CV <- function(data, K) {

N <- nrow(data)

# Dane przetasowane
data.rnd <- data[sample(1:N),]

# Tworzenie K pseudoprób
sets <- sapply(1:K, function(i) ((i-1) * (N/K) + 1):(i * (N/K)))

# Przypadek K = 1
if(is.vector(sets)) sets <- t(as.matrix(sets))

# Dla każdej pseudopróby wyznaczamy liczbę pomyłek
res <- t(sapply(1:K, function(k) CV.main(data.rnd[-c(sets[,k]),], data.rnd[sets[,k],])))

res
}

# Główna funkcja odpowiedzialna za CV
# przyjmuje PU (jedna z pseudoprób) oraz PT
CV.main <- function(learn, test) {

learn.classifier <- lda(class ~ ., data = learn)
test.pred <- predict(learn.classifier, newdata = test)

# Macierz pomyłek
CM <- table(test$class, test.pred$class)

# Liczba błędów
sum(CM) - sum(diag(CM))
}

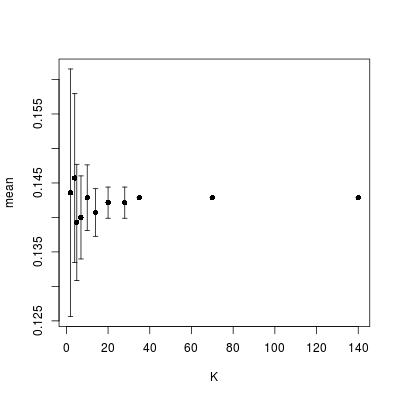
Aby przetestować działanie kroswalidacji na naszych danych, dokonamy jej 10-krotnie i dla każdego dzielnika (tzn. liczby, która dzieli oryginalne dane na całkowitą liczbę pseudoprób). Wyznaczymy wartości średne i odchylenia i korzystając z funkcji errorbar() z pakietu Hmisc (do instalacji), przekonamy się, jak różnią się wyniki

N <- nrow(data)

# Dzielniki N
div <- which(!(N %% 1:N))

# Wykonanie wielokrotnej CV dla różnych dzielników
mat <- sapply(div[-1], function(d) replicate(10, sum(CV(data, d)) / N))

# Wyznaczanie statystyk
cv.res <- as.data.frame(t(apply(mat, 2, function(x) c(mean(x), sd(x)))))
colnames(cv.res) <- c("mean", "sd")
cv.res$K <- div[-1]

library(Hmisc)

with(cv.res, errbar(K, mean, mean + sd, mean - sd))